《2025年全效学习同步学练测七年级数学上册湘教版》

变形 5 观察下列等式：$3^{1}=3$，$3^{2}=9$，$3^{3}=27$，$3^{4}=81$，$3^{5}=243$，$3^{6}=729$，$3^{7}=2187$，$\cdots$，则 $3 + 3^{2}+3^{3}+3^{4}+\cdots + 3^{2023}$ 的末位数字是(D)

A.$0$
B.$3$
C.$7$
D.$9$

答案： D

变形 6 若 $x$ 是不等于 $1$ 的实数，我们把 $\frac{1}{1 - x}$ 称为 $x$ 的“差倒数”，如 $3$ 的“差倒数”是 $\frac{1}{1 - 3}=-\frac{1}{2}$，$-\frac{1}{2}$ 的“差倒数”是 $\frac{1}{1 - (-\frac{1}{2})}=\frac{2}{3}$。现已知 $x_{1}=2$，$x_{2}$ 是 $x_{1}$ 的“差倒数”，$x_{3}$ 是 $x_{2}$ 的“差倒数”，$x_{4}$ 是 $x_{3}$ 的“差倒数”，$\cdots$，依此类推，则 $x_{2024}+x_{2025}$ 的和为(B)

A.$1$
B.$-\frac{1}{2}$
C.$\frac{5}{2}$
D.$-\frac{3}{2}$

答案： B

变形 7 已知整数 $a_{1}$，$a_{2}$，$a_{3}$，$a_{4}$，$\cdots$，满足下列条件：$a_{1}=0$，$a_{2}=-\vert a_{1}+1\vert$，$a_{3}=-\vert a_{2}+2\vert$，$a_{4}=-\vert a_{3}+3\vert$，$\cdots$，依此类推，则 $a_{2035}$ 的值为(D)

A.$-2035$
B.$2035$
C.$-1018$
D.$-1017$

答案： D

变形 8 观察算式：$3^{1}+2 = 5$，$3^{2}+2 = 11$，$3^{3}+2 = 29$，$3^{4}+2 = 83$，$3^{5}+2 = 245$，$3^{6}+2 = 731$，$\cdots$，则 $3^{2019}+2019$ 的个位数字是6。

答案： 6

变形 9 观察下列各式：
$1^{3}=1^{2}$；
$1^{3}+2^{3}=3^{2}$；
$1^{3}+2^{3}+3^{3}=6^{2}$；
$1^{3}+2^{3}+3^{3}+4^{3}=10^{2}$；
$\cdots$
猜想：$1^{3}+2^{3}+3^{3}+\cdots + 10^{3}=$55^2。

答案： $55^2$

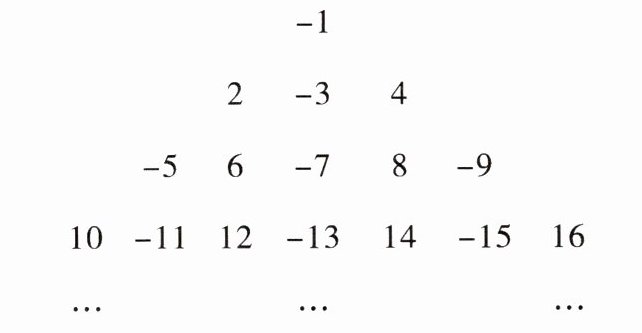
变形 10 观察一列数：$-1$，$2$，$-3$，$4$，$-5$，$6$，$-7$，$\cdots$，将这列数排成如图所示形式。记 $a_{ij}$ 对应的数为第 $i$ 行第 $j$ 列的数，如 $a_{23}=4$，那么 $a_{97}$ 对应的数为-71。

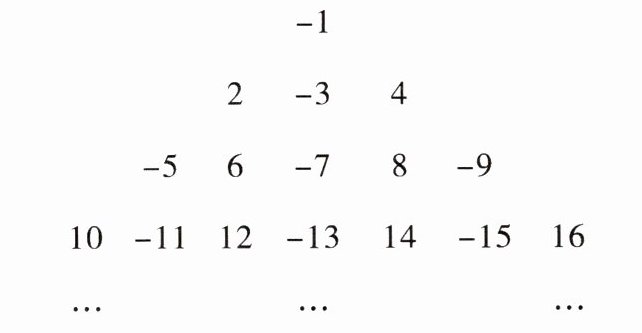
答案： -71

变形$ 11 $观察下面三行数：　　
$-2，$$4，$$-8，$$16，$$-32，$$64，$$\cdots，$$①$　　
$-5，$$1，$$-11，$$13，$$-35，$$61，$$\cdots，$$②$　　
$-\frac{1}{2}，$$1，$$-2，$$4，$$-8，$$16，$$\cdots，$$③$　　
$(1)$按第$①$行数排列的规律，第$①$行第$ n $个数是　　$(-2)^n$　　$($用含$ n $的式子表示$)；$　　
$(2)$取每行数的第$ 10 $个数，求这三个数的和。　　

答案：
$(1)(−2)^n$　　
$(2)$取每行数的第$10$个数，这三个数的和为$2301$