《2025年同步练习上海科学技术出版社八年级数学上册沪科版》

1. 若直线 $ kx - 3y = 8 $ 和 $ 2x + 5y = -4 $ 交点的纵坐标为 $ 0 $,则 $ k $ 的值为(B).
A.$ 4 $
B.$ -4 $
C.$ 2 $
D.$ -2 $

答案： B

2. 函数 $ y = 2x $ 和 $ y = ax + 4 $ 的图象交于点 $ A(m, 3) $,则关于 $ x $ 的方程 $ 2x = ax + 4 $ 的解为(A).
A.$ x = \frac{3}{2} $
B.$ x = 3 $
C.$ x = -\frac{3}{2} $
D.$ x = -3 $

答案： A

3. 将一张面值为 $ 100 $ 元的人民币兑换成面值为 $ 10 $ 元和 $ 20 $ 元的零钱,且两种零钱都要有,则兑换方案有(B)种.
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $

答案： B

4. 若直线 $ x + 2y + k + 1 = 0 $ 和直线 $ 2x + y + 2k = 0 $ 的交点在第三象限,则 $ k $ 的取值范围是$ k＞\frac{1}{3} $.

答案： $ k＞\frac{1}{3} $

5. 如图,直线 $ l_{甲} $,$ l_{乙} $ 分别表示甲走路与乙骑自行车(在同一条路上)行驶的路程 $ s \, m $ 与时间 $ t \, h $ 的关系,则两直线 $ l_{甲} $,$ l_{乙} $ 交点的实际意义是甲走2h与乙相遇.

答案： 甲走2h与乙相遇

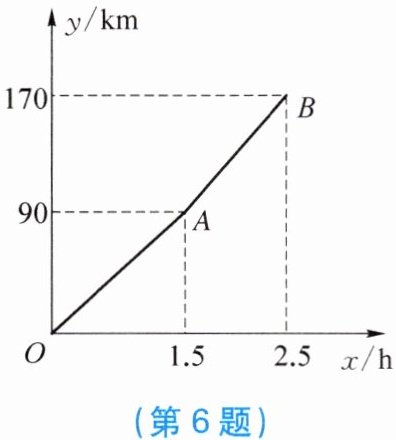
6. 五一期间,王老师一家自驾游去了离家 $ 170 \, km $ 的某地. 汽车行驶的距离 $ y \, km $ 与时间 $ x \, h $ 之间的函数图象如图所示. 当他们离目的地还有 $ 20 \, km $ 时,汽车一共行驶了2.25 $ h $.

答案： 2.25

7. 有两个发电厂,每焚烧 $ 1 \, t $ 垃圾,$ A $ 发电厂比 $ B $ 发电厂多发电 $ 40 \, kW \cdot h $,$ A $ 发电厂焚烧 $ 20 \, t $ 垃圾比 $ B $ 发电厂焚烧 $ 30 \, t $ 垃圾少发电 $ 1800 \, kW \cdot h $.
(1) 焚烧 $ 1 \, t $ 垃圾,$ A $,$ B $ 两发电厂分别发电多少？
(2) $ A $,$ B $ 两发电厂共焚烧 $ 90 \, t $ 垃圾,$ A $ 发电厂焚烧的垃圾不多于 $ B $ 发电厂焚烧的垃圾的 $ 2 $ 倍,求 $ A $,$ B $ 两发电厂总发电量的最大值.

答案： （1）A：300 kW·h，B：260 kW·h （2）25 800 kW·h