《2025年通成学典课时作业本八年级数学上册苏科版宿迁专版》

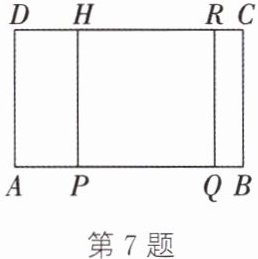
7. 如图,长方形ABCD的长$AB= 10\ cm$,宽$AD= 6\ cm$.正方形PQRH的四个顶点分别在边AB,CD上,将正方形PQRH向右平移.在这个平移过程中,下列结论正确的是( )


A.正方形的边长是变量
B.BQ的长是常量
C.长方形QBCR的面积随AP长度的变化而变化
D.长方形QBCR与长方形APHD的面积之和随AP长度的变化而变化

答案： C

8. 给出下列关于变量x,y的式子:①$3x-2y= 5$;②$y= |x|$;③$2x-y^{2}= 10$.其中,表示y是x的函数的为( )

A.①②③
B.①②
C.②③
D.①③

答案： B

9. 弹簧挂上物体后会伸长,测得一根弹簧的长度y(cm)与所挂物体的质量x(kg)有如下关系:
|x/kg|0|1|2|3|4|
|y/cm|12|12.5|13|13.5|14|
根据上述关系,回答下列问题:
(1)弹簧不挂物体时的长度是cm.
(2)当所挂物体的质量为1 kg时,弹簧伸长cm.
(3)给出下列各式:①$y+x= 12$;②$x= y-12$;③$y= 12+0.5x$;④$x= 12+0.5y$.其中,表示弹簧的长度y(cm)与所挂物体的质量x(kg)之间关系的式子为(填序号).
(4)当自变量x取10时的函数值为.

答案： （1）12 （2）0.5 （3）③ （4）17 解析:利用
(3)的结论,在$y=12+0.5x$中,令$x=10$,得$y=12+0.5×10=17$.

10. (2023·山西改编)如图所示的图案由边长相等的灰、白两色的正方形按一定规律拼接而成,设第n个图案中白色正方形的个数为S.
(1)S是n的函数吗? 如果是,请写出S与n之间的关系.
(2)是否存在这样的图案,使白色正方形的个数为2025? 如果存在,请指出是第几个图案;如果不存在,请说明理由.
...

答案： （1）是 $S=5n+3$ （2）不存在 理由:由题意,得$5n+3=2025$,解得$n=404.4$.
∵404.4不是正整数,
∴不存在这样的图案,使白色正方形的个数为2025.