《2025年通成学典课时作业本八年级数学上册苏科版宿迁专版》

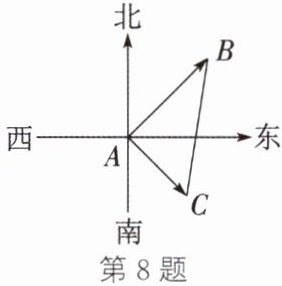
8. (2023·东营改编)如图,一艘轮船以16海里/时的速度从港口A出发向东北方向航行,同时,另一艘轮船以12海里/时的速度从港口A出发向东南方向航行.离开港口3小时后,两船相距( )

A.36海里
B.48海里
C.60海里
D.84海里

答案： C

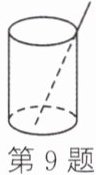
9. (2023·泗洪期中)如图,将一根长12cm的筷子置于底面直径为6cm,高为8cm的圆柱形杯子中,则筷子露在杯子外面的长度至少为______cm.

答案： 2

10. 如图,网格中每个小正方形的边长均为1,网格中有AB,CD,EF,GH四条线段(端点均在格点上).其中,能构成一个直角三角形的三条线段是______.

答案： AB,EF,GH

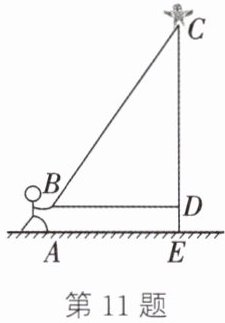
11. (2024·宿城期中)"儿童散学归来早,忙趁东风放纸鸢".又到了放风筝的最佳时节.如图,某校八年级(1)班的小明和小亮学习了"勾股定理"之后,为了测得风筝的垂直高度CE,他们进行了如下操作:① 测得水平距离BD为15m;② 根据手中剩余线的长度计算出风筝线BC的长为25m;③ 小明放风筝的手距地面的高度为1.6m.
(1)求风筝的垂直高度CE；
(2)若小明想风筝沿CD方向下降12m,则他应该往回收线多少米?

答案：
(1)在$Rt△CDB$中，由勾股定理，得$CD^{2}=BC^{2}-BD^{2}$，$\therefore CD=\sqrt{25^{2}-15^{2}} = 20(m)$，$\therefore CE = CD + DE = 20 + 1.6 = 21.6(m)$.答：风筝的垂直高度CE为21.6m
(2)设风筝沿CD方向下降12m后到点M处.由题意，得$CM = 12m$，$\therefore DM = 8m$，$\therefore$在$Rt△BDM$中，由勾股定理，得$BM=\sqrt{DM^{2}+BD^{2}}=\sqrt{8^{2}+15^{2}} = 17(m)$，$\therefore BC - BM = 25 - 17 = 8(m)$，$\therefore$他应该往回收线8m

12. 如图,圆柱形玻璃杯的高为16cm,底面周长为24cm.一只蚂蚁在杯外壁、离杯上沿5.5cm的点A处.蚂蚁发现,在与它相对的杯壁点B处有一滴蜂蜜,已知点B距离杯底5.5cm.
(1)若蜂蜜在杯外壁,则蚂蚁最少应爬行多远就能吃到蜂蜜?
(2)(2023·广安改编)若蜂蜜在杯内壁,蚂蚁要吃到蜂蜜,则最少应爬行多远(杯壁厚度不计)?

答案：
(1)如图①，过点A作$AH⊥MN$于点H，连接AB.由题意，得$AH = 12cm$，$BH = 16 - 2×5.5 = 5(cm)$.$\because AB^{2}=BH^{2}+AH^{2}$，$\therefore AB = 13cm$，$\therefore$若蜂蜜在杯外壁，则蚂蚁最少应爬行13cm就能吃到蜂蜜　
(2)如图②，作点A关于PM的对称点$A'$，过点$A'$作直线MN的垂线，垂足为D，连接$A'B$，易得$MD = PA' = PA = 5.5cm$，$BD = 16 - 5.5 + 5.5 = 16(cm)$，$A'D = 12cm$.$\because A'B^{2}=A'D^{2}+BD^{2}$，$\therefore A'B = 20cm$，$\therefore$若蜂蜜在杯内壁，蚂蚁要吃到蜂蜜，则最少应爬行20cm