《2025年通成学典课时作业本七年级数学上册苏科版宿迁专版》

9. (教材P164 练习第1题变式)请你仔细观察钟表并进行探究(填小于平角的角的度数).
(1)钟面上的时间为4时45分时,时针与分针的夹角的度数为______；
(2)当钟表上显示12时15分时,时针与分针的夹角的度数为______.

答案： 【解析】：
本题主要考察钟面角的知识点，即如何根据钟表上的时间计算时针与分针之间的夹角。
(1)对于4时45分的情况：
首先，我们知道分针每分钟转动$6^\circ$（因为一圈是$360^\circ$，分针60分钟转一圈，所以$\frac{360^\circ}{60} = 6^\circ$每分钟）。
到45分钟时，分针转动了$45 × 6^\circ = 270^\circ$。
时针每小时转动$30^\circ$（因为一圈是$360^\circ$，时针12小时转一圈，所以$\frac{360^\circ}{12} = 30^\circ$每小时）。
但时针也会随着分钟的增加而稍微移动，每分钟移动的角度是$\frac{30^\circ}{60} = 0.5^\circ$。
到4时45分时，时针转动了$4 × 30^\circ + 45 × 0.5^\circ = 120^\circ + 22.5^\circ = 142.5^\circ$。
因此，时针与分针的夹角为$270^\circ - 142.5^\circ = 127.5^\circ$。
(2)对于12时15分的情况：
分针到15分钟时转动了$15 × 6^\circ = 90^\circ$。
时针到12时15分时转动了$15 × 0.5^\circ = 7.5^\circ$（因为从12点开始，时针每小时的移动角度是0度，所以只需考虑分钟的移动）。
因此，时针与分针的夹角为$90^\circ - 7.5^\circ = 82.5^\circ$。
【答案】：
(1) $127.5^\circ$
(2) $82.5^\circ$

10. (1)如图,OA是表示北偏东36°方向的一条射线,射线OB表示北偏西45°方向(也称为西北方向)的一条射线；
(2)请在图中画出表示南偏西40°方向的射线OC、东南方向的射线OD.
（画图步骤：以点O为顶点，先确定南方向，向西偏转40°画出射线OC；再确定东南方向，即南偏东45°方向画出射线OD）

答案：
(1)北；西
(2)（画图步骤：以点O为顶点，先确定南方向，向西偏转40°画出射线OC；再确定东南方向，即南偏东45°方向画出射线OD）

11. (分类讨论思想)已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB= 80°,∠BOC= 30°.求∠AOC的度数.

答案： 【解析】：
本题主要考查角的概念与度量，特别是角的和与差。
由于射线$OB$和$OC$的位置关系不确定，因此需要分两种情况讨论：
当射线$OC$在$\angle AOB$内部时，$\angle AOC = \angle AOB - \angle BOC$。
当射线$OC$在$\angle AOB$外部时，$\angle AOC = \angle AOB + \angle BOC$。
根据这两种情况，可以分别计算出$\angle AOC$的度数。
【答案】：
解：
当射线$OC$在$\angle AOB$内部时：
$\angle AOC = \angle AOB - \angle BOC = 80{^\circ} - 30{^\circ} = 50{^\circ}$；
当射线$OC$在$\angle AOB$外部时：
$\angle AOC = \angle AOB + \angle BOC = 80{^\circ} + 30{^\circ} = 110{^\circ}$；
所以，$\angle AOC$的度数为$50{^\circ}$或$110{^\circ}$。

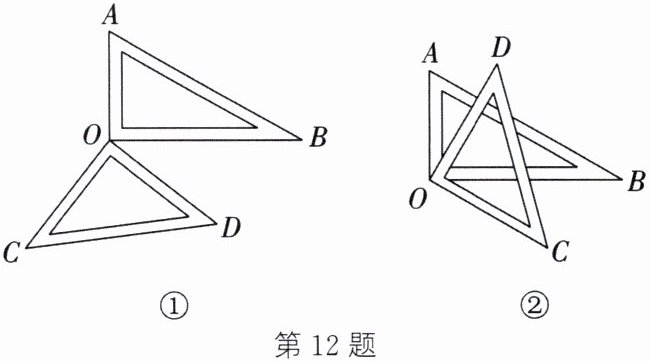
12. (1)如图①,将一副直角三角尺的直角顶点重合在点O处.
① ∠AOD与∠BOC的数量关系是相等；
② ∠AOC与∠BOD的数量关系是互补.
(2)若将这副直角三角尺按如图②所示的方式摆放,使三角尺的直角顶点重合在点O处.∠AOD与∠BOC有什么数量关系?∠AOC与∠BOD又有什么数量关系?请分别说明理由.
]
∠AOD=∠BOC，理由如下：
∵∠AOB=∠COD=90°
∴∠AOB-∠BOD=∠COD-∠BOD
即∠AOD=∠BOC
∠AOC+∠BOD=180°，理由如下：
∵∠AOB=∠COD=90°
∴∠AOC=∠AOB+∠BOC=90°+∠BOC
∴∠AOC+∠BOD=90°+∠BOC+∠BOD=90°+∠COD=90°+90°=180°

答案：
(1)①相等
②互补
(2)∠AOD=∠BOC，理由如下：
∵∠AOB=∠COD=90°
∴∠AOB-∠BOD=∠COD-∠BOD
即∠AOD=∠BOC
∠AOC+∠BOD=180°，理由如下：
∵∠AOB=∠COD=90°
∴∠AOC=∠AOB+∠BOC=90°+∠BOC
∴∠AOC+∠BOD=90°+∠BOC+∠BOD=90°+∠COD=90°+90°=180°