1. 如图,比数轴上点A表示的数大3的数是(
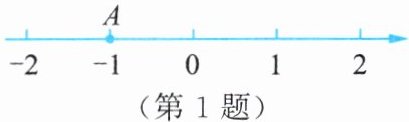
A.-1
B.0
C.1
D.2
]
D
)。
A.-1
B.0
C.1
D.2
]
答案:
D
2. 下列计算正确的是(
A.$\frac{1}{3}-\frac{1}{3}× 4= 0× 4= 0$
B.$4÷ (-2)× (-\frac{1}{2})= 4÷ 1= 4$
C.$-3^{2}-(-2)^{3}= 9-8= 1$
D.$(-\frac{1}{4})÷ (\frac{1}{12}+\frac{1}{16})= (-\frac{1}{4})÷ \frac{7}{48}= -\frac{12}{7}$
D
)。A.$\frac{1}{3}-\frac{1}{3}× 4= 0× 4= 0$
B.$4÷ (-2)× (-\frac{1}{2})= 4÷ 1= 4$
C.$-3^{2}-(-2)^{3}= 9-8= 1$
D.$(-\frac{1}{4})÷ (\frac{1}{12}+\frac{1}{16})= (-\frac{1}{4})÷ \frac{7}{48}= -\frac{12}{7}$
答案:
D
3. 计算:
(1)$-6+4$;
(2)$(-7)-(-13)$;
(3)$(-\frac{11}{5})× (-\frac{2}{11})$;
(4)$36÷ (-\frac{1}{3})$。
(1)$-6+4$;
(2)$(-7)-(-13)$;
(3)$(-\frac{11}{5})× (-\frac{2}{11})$;
(4)$36÷ (-\frac{1}{3})$。
答案:
1. (1)
解:$-6 + 4=-(6 - 4)=-2$。
2. (2)
解:$(-7)-(-13)=-7 + 13=13 - 7 = 6$。
3. (3)
解:$(-\frac{11}{5})×(-\frac{2}{11})=\frac{11}{5}×\frac{2}{11}=\frac{2}{5}$。
4. (4)
解:$36÷(-\frac{1}{3})=36×(-3)=-108$。
综上,答案依次为:(1)$-2$;(2)$6$;(3)$\frac{2}{5}$;(4)$-108$。
解:$-6 + 4=-(6 - 4)=-2$。
2. (2)
解:$(-7)-(-13)=-7 + 13=13 - 7 = 6$。
3. (3)
解:$(-\frac{11}{5})×(-\frac{2}{11})=\frac{11}{5}×\frac{2}{11}=\frac{2}{5}$。
4. (4)
解:$36÷(-\frac{1}{3})=36×(-3)=-108$。
综上,答案依次为:(1)$-2$;(2)$6$;(3)$\frac{2}{5}$;(4)$-108$。
4. 计算:
(1)$(-\frac{1}{2})+(+\frac{3}{5})-\frac{3}{2}$;
(2)$4+3× (-2)^{3}$;
(3)$-4.2÷ \frac{7}{8}× (-\frac{5}{4})$;
(4)$(-6)^{2}× (\frac{1}{3}-\frac{1}{2})-2^{3}$。
(1)$(-\frac{1}{2})+(+\frac{3}{5})-\frac{3}{2}$;
(2)$4+3× (-2)^{3}$;
(3)$-4.2÷ \frac{7}{8}× (-\frac{5}{4})$;
(4)$(-6)^{2}× (\frac{1}{3}-\frac{1}{2})-2^{3}$。
答案:
1. (1)
解:
利用加法交换律$a + b + c=a + c + b$,则$(-\frac{1}{2})+(+\frac{3}{5})-\frac{3}{2}=(-\frac{1}{2}-\frac{3}{2})+\frac{3}{5}$。
先计算$-\frac{1}{2}-\frac{3}{2}$,根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$(这里$c = 2$,$a=-1$,$b = 3$),$-\frac{1}{2}-\frac{3}{2}=\frac{-1 - 3}{2}=\frac{-4}{2}=-2$。
再计算$-2+\frac{3}{5}$,根据异分母分数加法法则$a+\frac{b}{c}=\frac{ac + b}{c}$(这里$a=-2=\frac{-10}{5}$,$b = 3$,$c = 5$),$-2+\frac{3}{5}=\frac{-10 + 3}{5}=-\frac{7}{5}$。
2. (2)
解:
先计算指数运算$(-2)^{3}$,根据$a^{n}$($a=-2$,$n = 3$)的定义$a^{n}=\underbrace{a× a×\cdots× a}_{n个a}$,则$(-2)^{3}=(-2)×(-2)×(-2)=-8$。
再计算乘法运算$3×(-8)$,根据有理数乘法法则$a× b$($a = 3$,$b=-8$),异号得负,$3×(-8)=-24$。
最后计算加法运算$4+( - 24)$,根据有理数加法法则$a+( - b)=a - b$($a = 4$,$b = 24$),$4+( - 24)=4-24=-20$。
3. (3)
解:
先将$-4.2$化为分数$-4.2=-\frac{42}{10}=-\frac{21}{5}$。
再根据除法运算法则$a÷ b=a×\frac{1}{b}$($a =-\frac{21}{5}$,$b=\frac{7}{8}$),则$-4.2÷\frac{7}{8}=-\frac{21}{5}×\frac{8}{7}$。
计算$-\frac{21}{5}×\frac{8}{7}$,根据分数乘法法则$\frac{a}{b}×\frac{c}{d}=\frac{ac}{bd}$($a=-21$,$b = 5$,$c = 8$,$d = 7$),$-\frac{21}{5}×\frac{8}{7}=\frac{-21×8}{5×7}=\frac{-3×8}{5}=-\frac{24}{5}$。
然后计算$-\frac{24}{5}×(-\frac{5}{4})$,根据分数乘法法则,同号得正,$\frac{24×5}{5×4}=6$。
4. (4)
解:
先计算指数运算$(-6)^{2}=36$,$2^{3}=8$。
再计算括号内的运算$\frac{1}{3}-\frac{1}{2}$,根据异分母分数减法法则$\frac{a}{c}-\frac{b}{d}=\frac{ad - bc}{cd}$($a = 1$,$b = 1$,$c = 3$,$d = 2$),$\frac{1}{3}-\frac{1}{2}=\frac{2-3}{6}=-\frac{1}{6}$。
然后计算乘法运算$36×(-\frac{1}{6})$,根据有理数乘法法则$a× b$($a = 36$,$b=-\frac{1}{6}$),异号得负,$36×(-\frac{1}{6})=-6$。
最后计算减法运算$-6-8$,根据有理数减法法则$a - b=a+( - b)$,$-6-8=-6+( - 8)=-14$。
综上,(1)$-\frac{7}{5}$;(2)$-20$;(3)$6$;(4)$-14$。
解:
利用加法交换律$a + b + c=a + c + b$,则$(-\frac{1}{2})+(+\frac{3}{5})-\frac{3}{2}=(-\frac{1}{2}-\frac{3}{2})+\frac{3}{5}$。
先计算$-\frac{1}{2}-\frac{3}{2}$,根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$(这里$c = 2$,$a=-1$,$b = 3$),$-\frac{1}{2}-\frac{3}{2}=\frac{-1 - 3}{2}=\frac{-4}{2}=-2$。
再计算$-2+\frac{3}{5}$,根据异分母分数加法法则$a+\frac{b}{c}=\frac{ac + b}{c}$(这里$a=-2=\frac{-10}{5}$,$b = 3$,$c = 5$),$-2+\frac{3}{5}=\frac{-10 + 3}{5}=-\frac{7}{5}$。
2. (2)
解:
先计算指数运算$(-2)^{3}$,根据$a^{n}$($a=-2$,$n = 3$)的定义$a^{n}=\underbrace{a× a×\cdots× a}_{n个a}$,则$(-2)^{3}=(-2)×(-2)×(-2)=-8$。
再计算乘法运算$3×(-8)$,根据有理数乘法法则$a× b$($a = 3$,$b=-8$),异号得负,$3×(-8)=-24$。
最后计算加法运算$4+( - 24)$,根据有理数加法法则$a+( - b)=a - b$($a = 4$,$b = 24$),$4+( - 24)=4-24=-20$。
3. (3)
解:
先将$-4.2$化为分数$-4.2=-\frac{42}{10}=-\frac{21}{5}$。
再根据除法运算法则$a÷ b=a×\frac{1}{b}$($a =-\frac{21}{5}$,$b=\frac{7}{8}$),则$-4.2÷\frac{7}{8}=-\frac{21}{5}×\frac{8}{7}$。
计算$-\frac{21}{5}×\frac{8}{7}$,根据分数乘法法则$\frac{a}{b}×\frac{c}{d}=\frac{ac}{bd}$($a=-21$,$b = 5$,$c = 8$,$d = 7$),$-\frac{21}{5}×\frac{8}{7}=\frac{-21×8}{5×7}=\frac{-3×8}{5}=-\frac{24}{5}$。
然后计算$-\frac{24}{5}×(-\frac{5}{4})$,根据分数乘法法则,同号得正,$\frac{24×5}{5×4}=6$。
4. (4)
解:
先计算指数运算$(-6)^{2}=36$,$2^{3}=8$。
再计算括号内的运算$\frac{1}{3}-\frac{1}{2}$,根据异分母分数减法法则$\frac{a}{c}-\frac{b}{d}=\frac{ad - bc}{cd}$($a = 1$,$b = 1$,$c = 3$,$d = 2$),$\frac{1}{3}-\frac{1}{2}=\frac{2-3}{6}=-\frac{1}{6}$。
然后计算乘法运算$36×(-\frac{1}{6})$,根据有理数乘法法则$a× b$($a = 36$,$b=-\frac{1}{6}$),异号得负,$36×(-\frac{1}{6})=-6$。
最后计算减法运算$-6-8$,根据有理数减法法则$a - b=a+( - b)$,$-6-8=-6+( - 8)=-14$。
综上,(1)$-\frac{7}{5}$;(2)$-20$;(3)$6$;(4)$-14$。
查看更多完整答案,请扫码查看


