第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
1. 直接写出得数。
$25×4=$
$5×24=$
$25×4=$
100
$6×15=$90
$25×8=$200
$26×3=$78
$5×24=$
120
$16×5=$80
$8×15=$120
$35×4=$140
答案:
分析:
这是一道口算题目,主要考查的是基础的乘法运算。题目中给出的乘法表达式都比较简单,可以直接进行计算得出结果。
答案:
$25×4=100$
$6×15=90$
$25×8=200$
$26×3=78$
$5×24=120$
$16×5=80$
$8×15=120$
$35×4=140$
这是一道口算题目,主要考查的是基础的乘法运算。题目中给出的乘法表达式都比较简单,可以直接进行计算得出结果。
答案:
$25×4=100$
$6×15=90$
$25×8=200$
$26×3=78$
$5×24=120$
$16×5=80$
$8×15=120$
$35×4=140$
2. 想一想,填一填,并完成计算。




答案:
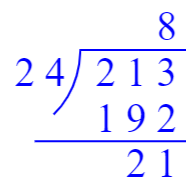
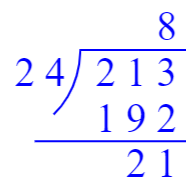
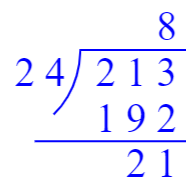
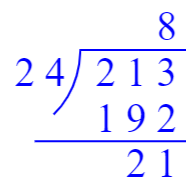
3. 列竖式计算,带“★”的题要验算。
$235÷35=$
$235÷35=$
6……25
$120÷14=$8……8
★$384÷46=$8……16
答案:
235÷35=6……25
120÷14=8……8
384÷46=8……16
120÷14=8……8
384÷46=8……16
4. 下表是某超市今年9月1日一些商品的销售情况。
|商品|单价|总价|
|钢笔|34元/支|136元|
|书包|66元/个|330元|
|水彩笔|19元/盒|152元|
(1) 这一天中,(
(2) 杨老师带了260元钱,去该超市买钢笔,最多可以买多少支?
|商品|单价|总价|
|钢笔|34元/支|136元|
|书包|66元/个|330元|
|水彩笔|19元/盒|152元|
(1) 这一天中,(
水彩笔
)的销售数量最多。(2) 杨老师带了260元钱,去该超市买钢笔,最多可以买多少支?
7支
答案:
解析:本题主要考查总价公式的应用及除法的运算。
(1)首先,需要计算每种商品的销售数量。
销售数量等于总价除以单价。
钢笔的销售数量为:$136 ÷ 34 = 4(支)$。
书包的销售数量为:$330 ÷ 66 = 5(个)$。
水彩笔的销售数量为:$152 ÷ 19 = 8(盒)$。
比较这三种商品的销售数量,可以发现水彩笔的销售数量最多,为8盒。
答案:
(1)这一天中,水彩笔的销售数量最多。
(2)杨老师带了260元钱去超市买钢笔,需要计算他最多可以买多少支钢笔。
这可以通过将杨老师带的钱数除以钢笔的单价来得出:$260 ÷ 34 = 7(支)\dots\dots 22(元)$。
因为余下的22元不足以再购买一支钢笔,所以杨老师最多可以买7支钢笔。
答案:
(2)杨老师带了260元钱,去该超市买钢笔,最多可以买7支。
(1)首先,需要计算每种商品的销售数量。
销售数量等于总价除以单价。
钢笔的销售数量为:$136 ÷ 34 = 4(支)$。
书包的销售数量为:$330 ÷ 66 = 5(个)$。
水彩笔的销售数量为:$152 ÷ 19 = 8(盒)$。
比较这三种商品的销售数量,可以发现水彩笔的销售数量最多,为8盒。
答案:
(1)这一天中,水彩笔的销售数量最多。
(2)杨老师带了260元钱去超市买钢笔,需要计算他最多可以买多少支钢笔。
这可以通过将杨老师带的钱数除以钢笔的单价来得出:$260 ÷ 34 = 7(支)\dots\dots 22(元)$。
因为余下的22元不足以再购买一支钢笔,所以杨老师最多可以买7支钢笔。
答案:
(2)杨老师带了260元钱,去该超市买钢笔,最多可以买7支。
5. 东东在做计算题时,把“$171÷\Box$”错写成“$117÷\Box$”,所得的商比正确的商少3,但余数没变。正确的除数和余数分别是多少?
除数是18,余数是9。
答案:
解析:
本题考查的是有余数的除法各部分之间的关系。
假设正确的除数为$d$,余数为$r$。
根据除法的定义,可以得出以下两个等式:
$171 = qd + r$ (正确的商为$q$)
$117 = (q-3)d + r$ (错误的商比正确的商少3)
从第一个等式中,可以得到:
$qd = 171 - r$
从第二个等式中,可以得到:
$(q-3)d = 117 - r$
将两个等式相减,得到:
$3d = 54$
解得:
$d = 18$
将$d = 18$代入$171 = qd + r$中,得到:
$171 = 18q + r$
由于$117 = (q-3)d + r$,可以转化为:
$117 = 18(q-3) + r$
$117 = 18q - 54 + r$
与上面的等式相减,得到:
$54 = 54 + r - r$ (这一步是为了验证$r$在两个等式中是一致的)
同时,从$171 = 18q + r$中,可以尝试找出$q$和$r$的值。
由于$r$必须小于$d$,即$r < 18$,可以通过试除法得到:
$171 ÷ 18 = 9$ 余 $9$
所以,正确的商$q = 9 + 3 = 12$(因为错误的商少了3),余数$r = 9$。
但由于我们之前已经通过代数方法得到了除数$d$,所以只需要验证余数即可。
综上,正确的除数是18,余数是9。
答案:
除数是18,余数是9。
本题考查的是有余数的除法各部分之间的关系。
假设正确的除数为$d$,余数为$r$。
根据除法的定义,可以得出以下两个等式:
$171 = qd + r$ (正确的商为$q$)
$117 = (q-3)d + r$ (错误的商比正确的商少3)
从第一个等式中,可以得到:
$qd = 171 - r$
从第二个等式中,可以得到:
$(q-3)d = 117 - r$
将两个等式相减,得到:
$3d = 54$
解得:
$d = 18$
将$d = 18$代入$171 = qd + r$中,得到:
$171 = 18q + r$
由于$117 = (q-3)d + r$,可以转化为:
$117 = 18(q-3) + r$
$117 = 18q - 54 + r$
与上面的等式相减,得到:
$54 = 54 + r - r$ (这一步是为了验证$r$在两个等式中是一致的)
同时,从$171 = 18q + r$中,可以尝试找出$q$和$r$的值。
由于$r$必须小于$d$,即$r < 18$,可以通过试除法得到:
$171 ÷ 18 = 9$ 余 $9$
所以,正确的商$q = 9 + 3 = 12$(因为错误的商少了3),余数$r = 9$。
但由于我们之前已经通过代数方法得到了除数$d$,所以只需要验证余数即可。
综上,正确的除数是18,余数是9。
答案:
除数是18,余数是9。
查看更多完整答案,请扫码查看


