《2025年作业本浙江教育出版社四年级数学上册人教版》

6. 某商场搞促销活动,一种盒装巧克力,原价是128元/盒,现在买3盒送1盒。小王买了4盒这样的巧克力,每盒的实际价格是多少元?相当于每盒降价多少元?

答案： 解析：
题目考查的是单价、数量、总价之间的关系。
需要用到除法来计算每盒的实际价格，以及通过比较原价和实际价格来计算每盒的降价金额。
首先，计算小王买4盒巧克力的总价，由于买3盒送1盒，所以实际支付的只是3盒的价格，即$128 × 3 = 384(元)$。
然后，计算每盒巧克力的实际价格，即总价除以4盒，$384 ÷ 4 = 96(元)$。
最后，比较原价和实际价格，计算每盒的降价金额，即$128 - 96 = 32(元)$。
答案：
每盒的实际价格是96元。
相当于每盒降价32元。

7. 小林每天早上以85米/分的速度步行上学,18分钟可以到达学校。放学时妈妈骑电瓶车来接他,电瓶车的速度是多少?

答案： 解析：本题考查路程、速度和时间的关系，先根据上学时的速度和时间求出家到学校的距离，再根据回家时间求出电瓶车速度。
1. 求小林家到学校的距离：
根据公式：$路程 = 速度×时间$，已知上学速度为$85$米/分，时间是$18$分钟，所以小林家到学校的距离为$85×18 = 1530$（米）。
2. 求电瓶车的速度：
已知放学回家用了$6$分钟，路程为$1530$米，根据公式：$速度 = 路程÷时间$，可得电瓶车速度为$1530÷6 = 255$（米/分）。
答案：$255$米/分。

8. 如右图,小林和小丽同时从家里出发向对方家走去。15分钟后,他们在途中的某处相遇。

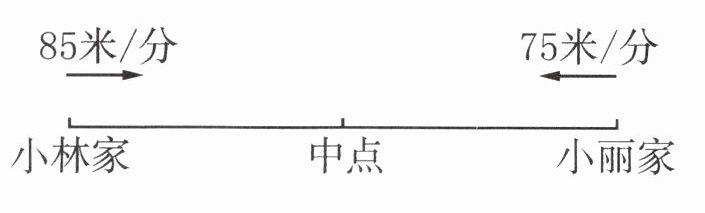
(1) 在图上标出他们相遇时的大致位置。
(2) 小林家和小丽家的距离是多少米?
(3) 从出发到相遇,小林比小丽多走多少米?

答案：

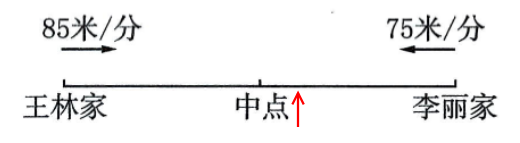
(1)
(2)85×15+75×15=2400 (米)

答：王林家和李丽家的距离是2400米。

(3)85×15-75×15=150 (米)

答：王林比李丽多行走了150米。

9. 购买同样价格的课桌,第一次买12张,第二次买21张,两次花的钱相差1350元。
(1) 两次的总价相差1350元,是因为课桌的数量相差9张。
(2) 课桌的单价是多少?150元(3) 两次买课桌共花了多少元钱?4950元

答案： 解析：
(1) 题目考查的是两次购买课桌数量的差值，通过简单的减法计算即可得出。
(2) 通过已知两次购买课桌的数量差和总价差，利用除法可以求出课桌的单价。
(3) 在求出课桌单价的基础上，通过乘法计算出两次购买课桌的总花费。
答案：
(1) 两次的课桌数量相差：$21 - 12 = 9$(张)
所以，两次的总价相差1350元，是因为课桌的数量相差9张。
(2) 课桌的单价可以通过总价差除以数量差来求得：
单价 $= 1350 ÷ 9 = 150$(元)
所以，课桌的单价是150元。
(3) 两次买课桌的总花费可以通过单价乘以两次购买的总数量来求得：
总花费 $= 150 × (12 + 21) = 150 × 33 = 4950$(元)
所以，两次买课桌共花了4950元。