第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
1. 直接写出得数。
$60×40= $
$40×25= $
$60×40= $
2400
$70×50= $3500
$40×15= $600
$160×7= $1120
$40×25= $
1000
$30×67= $2010
$150×60= $9000
$880×50= $44000
答案:
解析:
这些题目都是基础的乘法口算题,主要考查学生对于乘法运算的熟练程度。
答案:
$60×40= 2400$
$70×50= 3500$
$40×15= 600$
$160×7= 1120$
$40×25= 1000$
$30×67= 2010$
$150×60= 9000$
$880×50= 44000$
这些题目都是基础的乘法口算题,主要考查学生对于乘法运算的熟练程度。
答案:
$60×40= 2400$
$70×50= 3500$
$40×15= 600$
$160×7= 1120$
$40×25= 1000$
$30×67= 2010$
$150×60= 9000$
$880×50= 44000$
2. 根据$25×24= 600$,把下面的算式填写完整。
$75×(
$75×(
24
)= 1800$ $25×(12
)= 300$ $(50
)×12= 600$
答案:
75×
(24)=1800
25×
(12)=300
(50)×12=600
(24)=1800
25×
(12)=300
(50)×12=600
(1) 下列选项中,用$240÷8$求单价的是(
A.8筐苹果共有240个,每筐有多少个
B.用240元购买8元/千克的大米,可以买多少千克
C.买8份同样的快餐,共花了240元,每份快餐多少元
C
)。A.8筐苹果共有240个,每筐有多少个
B.用240元购买8元/千克的大米,可以买多少千克
C.买8份同样的快餐,共花了240元,每份快餐多少元
答案:
解析:本题考查的知识点是单价、数量、总价之间的关系。
选项A:已知8筐苹果的总数为240个,求每筐的数量,是求数量,用总数除以份数,列式为$240÷ 8$,不符合题意。
选项B:已知总价是240元,单价是8元/千克,求数量,根据“数量=总价÷单价”得列式为$240÷ 8$,不符合题意。
选项C:买了8份同样的快餐,共花了240元,求每份快餐的价格,是求单价,根据公式“单价=总价÷数量”,可列式为$240÷ 8$,符合题意。
答案:C。
选项A:已知8筐苹果的总数为240个,求每筐的数量,是求数量,用总数除以份数,列式为$240÷ 8$,不符合题意。
选项B:已知总价是240元,单价是8元/千克,求数量,根据“数量=总价÷单价”得列式为$240÷ 8$,不符合题意。
选项C:买了8份同样的快餐,共花了240元,求每份快餐的价格,是求单价,根据公式“单价=总价÷数量”,可列式为$240÷ 8$,符合题意。
答案:C。
(2) 下列选项中,速度最快的是(
A.10米/秒
B.1分钟行85米
C.8分钟走了1千米
A
)。A.10米/秒
B.1分钟行85米
C.8分钟走了1千米
答案:
A选项速度为10米/秒。
B选项:1分钟=60秒,85÷60≈1.42米/秒。
C选项:1千米=1000米,8分钟=480秒,1000÷480≈2.08米/秒。
10>2.08>1.42,所以速度最快的是A。
答案:A
B选项:1分钟=60秒,85÷60≈1.42米/秒。
C选项:1千米=1000米,8分钟=480秒,1000÷480≈2.08米/秒。
10>2.08>1.42,所以速度最快的是A。
答案:A
4. 用数字卡片$\boxed{0}\boxed{2}\boxed{4}\boxed{6}\boxed{8}$按要求组成三位数乘两位数的算式。
(1) 积最大的算式是(
(2) 如果希望积接近一万,算式可以是(
(1) 积最大的算式是(
820×64
)。(2) 如果希望积接近一万,算式可以是(
208×46
)。
答案:
(1) 820×64=52480(或840×62=52080、640×82=52480、620×84=52080,积最大为52480,算式可写820×64或640×82)
(2) 208×46=9568(或206×48=9888、248×40=9920等,合理即可)
(1) 820×64=52480(或840×62=52080、640×82=52480、620×84=52080,积最大为52480,算式可写820×64或640×82)
(2) 208×46=9568(或206×48=9888、248×40=9920等,合理即可)
5. 列竖式计算。
$675×33= $ $54×305= $ $360×38= $
$675×33= $ $54×305= $ $360×38= $
答案:
解析:
题目要求列竖式计算几个乘法表达式,这涉及到多位数乘法的运算。在乘法竖式中,我们需要将一个乘数的每一位分别与另一个乘数相乘,然后将得到的结果相加,最后得出最终的乘积。
答案:
$675 × 33 = 22275$
$54 × 305 = 16470$
$360 × 38 = 13680$
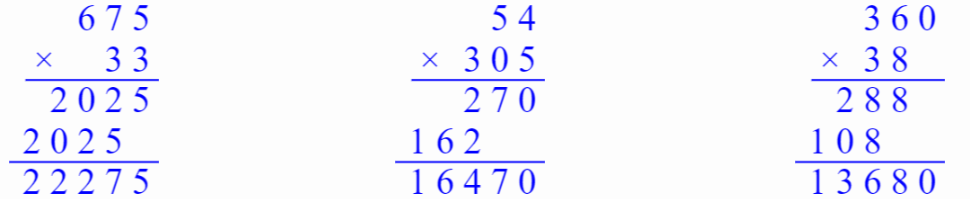
解析:
题目要求列竖式计算几个乘法表达式,这涉及到多位数乘法的运算。在乘法竖式中,我们需要将一个乘数的每一位分别与另一个乘数相乘,然后将得到的结果相加,最后得出最终的乘积。
答案:
$675 × 33 = 22275$
$54 × 305 = 16470$
$360 × 38 = 13680$
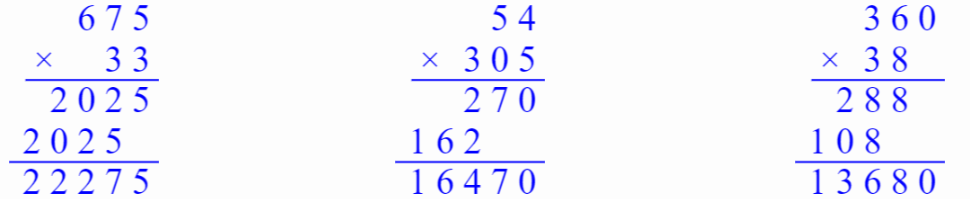
查看更多完整答案,请扫码查看


