《2025年作业本浙江教育出版社四年级数学上册人教版》

1. 写出下面各角的名称。

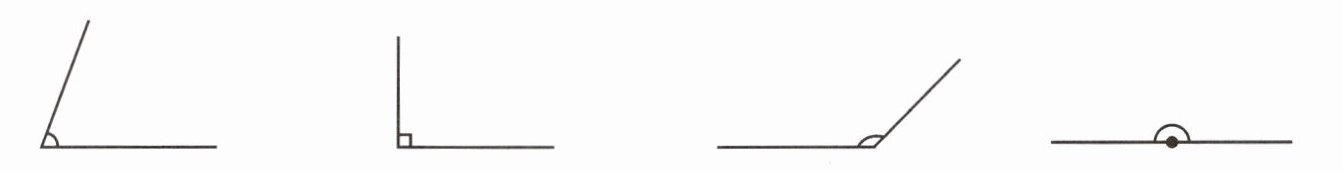
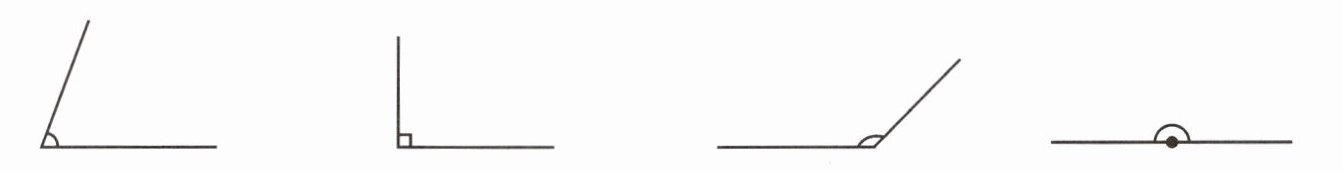
(锐)角 (直)角 (钝)角 (平)角

答案： 本题可根据角的分类及各类角的定义来判断图中各角的名称。
角的分类及定义
锐角：大于$0^{\circ}$而小于$90^{\circ}$的角叫做锐角。
直角：等于$90^{\circ}$的角叫做直角。
钝角：大于$90^{\circ}$而小于$180^{\circ}$的角叫做钝角。
平角：等于$180^{\circ}$的角叫做平角。
判断各角的名称
第一个角：该角的度数大于$0^{\circ}$而小于$90^{\circ}$，根据锐角的定义可知，这个角是锐角。
第二个角：该角的度数等于$90^{\circ}$，根据直角的定义可知，这个角是直角。
第三个角：该角的度数大于$90^{\circ}$而小于$180^{\circ}$，根据钝角的定义可知，这个角是钝角。
第四个角：该角的度数等于$180^{\circ}$，根据平角的定义可知，这个角是平角。
综上，答案依次为：锐；直；钝；平。

2. 看钟面,填写时针与分针组成的角的度数,并写出角的名称。

(90)° (180)° (60)° (120)°
(直角)角 (平角)角 (锐角)角 (钝角)角

答案： 90° 180° 60° 120°
直角 平角 锐角 钝角

3. 填一填。
(1)一条射线绕着它的端点旋转180°,形成的角是平角。
(2)大于90°而小于180°的角是钝角。
(3)把一个钝角分成两个角,其中一个是锐角,另一个可能是锐角,也可能是直角角,还可能是钝角角。

答案： 解析：
(1) 题目考查的是对平角概念的理解。当一条射线绕着它的端点旋转180°时，它会形成一个平角。
(2) 题目考查的是对钝角定义的理解。大于90°而小于180°的角被定义为钝角。
(3) 题目考查的是对角的分裂和角的大小的理解。钝角可以被分成两个角，其中一个角是锐角，另一个角的大小取决于分裂的方式。如果分裂得较为均匀，可能得到另一个锐角；如果分裂得不均匀，可能得到一个直角或一个钝角。
答案：
(1) 平角
(2) 钝角
(3) 直角，钝角

4. 把一张圆形纸对折3次,可以得到哪些度数的角?想一想,填一填。
180；90；45

答案： 解析：本题主要考查对折后角度的计算。
将圆对折$1$次，得到的是以圆心为顶点，半径为边的平角，度数为$180^{\circ}$；
对折$2$次，就是把$180^{\circ}$的角再平均分成$2$份，$180^{\circ}÷2 = 90^{\circ}$，得到的是直角；
对折$3$次，就是把$90^{\circ}$的角再平均分成$2$份，$90^{\circ}÷2 = 45^{\circ}$，得到的是锐角。
答案：$180$；$90$；$45$。

*5. 如右图,将两个相同的长方形叠起来。
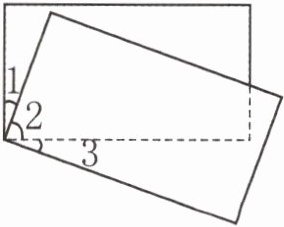
已知∠1+∠2+∠3= 110°,那么
∠2= (70)°,∠3= (20)°。

答案： ∠1+∠2=90°，∠2+∠3=90°，所以∠1=∠3。
∠1+∠2+∠3=110°，∠1+∠3=110°-∠2，又因为∠1=∠3，所以2∠1=110°-∠2。
因为∠1=90°-∠2，所以2×(90°-∠2)=110°-∠2，180°-2∠2=110°-∠2，∠2=70°。
∠3=90°-∠2=90°-70°=20°。
∠2=70°，∠3=20°