《2025年作业本浙江教育出版社四年级数学上册人教版》

$99999×11=1099989$
$99999×15=1499985$
$99999×12=1199988$
$99999×16=1599984$
$99999×13=1299987$
$99999×17=1699983$
$99999×14=1399986$
$99999×18=1799982$

答案： 解析：
本题主要考察的是乘法运算以及规律的寻找。
首先，我们使用计算器来计算左边各题的答案，然后观察规律，以便直接写出右边各题的答案。
通过观察，我们可以发现，当99999乘以一个比10大的数时，结果的最高位是乘数减1，接下来的几位都是9，9的个数比乘数的个位数少1，最后一位是10减去乘数的个位数。
答案:
$99999 × 11 = 1099989$
$99999 × 15 = 1499985$
根据规律，我们可以直接写出：
$99999 × 12 = 1199988$
$99999 × 16 = 1599984$
$99999 × 13 = 1299987$
$99999 × 17 = 1699983$
$99999 × 14 = 1399986$
$99999 × 18 = 1799982$

$12345679×54= (666666666)$
$555555555÷12345679= (45)$

答案： 解析：
本题考查的是利用规律进行计算。
首先，观察给出的算式 $12345679 × 9 = 111111111$。
这里，12345679 乘以 9 得到了一个全部由 1 组成的九位数。
接下来，分析 $12345679 × 54$：
由于 $54 = 9 × 6$，可以将 $12345679 × 54$ 分解为 $12345679 × 9 × 6$。
已知 $12345679 × 9 = 111111111$，所以只需将这个结果乘以 6 即可。
$111111111 × 6 = 666666666$
再来看 $555555555 ÷ 12345679$：
由于 $555555555$ 是由 5 组成的九位数，且位数与 $111111111$ 相同，可以尝试将其分解为 $111111111 × 5$。
那么，$555555555 ÷ 12345679$ 就等于 $(111111111 × 5) ÷ 12345679$。
由于 $111111111 ÷ 12345679 = 9$，所以最终结果是 $9 × 5 = 45$ 的其中一个因数，即 45 除以 9（12345679乘9得111111111）的结果，也就是 45 里面包含几个 9，显然是 5-0=4+1=5（个）中 9 的个数，直接得出：
$555555555 ÷ 12345679 = 45 ÷ 9 × (111111111 ÷ 111111111的商1省略) = 5 × 1 × (9 ÷ 9) = 5 × 1 = 45 ÷ (9 ÷ 1) = 45 ÷ 9 × 1 = 5$
或者直接通过除法关系得出：
$555555555 ÷ 111111111 = 5$，而 $111111111 ÷ 12345679 = 9$，所以 $555555555 ÷ 12345679 = 5 × 9 ÷ 9 = 5$。
答案：$666666666$；$45$。

3. 计算:$1+2+3+4+5+... +100= $5050。这道题你打算用计算器计算吗?不打算。理由:因为可以利用等差数列求和公式$\frac{n(a_1 + a_n)}{2}$来简便计算，其中$n = 100$，$a_1=1$，$a_n = 100$，代入可得$\frac{100×(1 + 100)}{2}=5050$，比用计算器逐步相加更简便。

答案： 解析：本题考查加法结合律的应用以及等差数列求和公式。
加法结合律：$a+b+c=a+(b+c)$。
这里加数是从$1$到$100$的连续自然数，构成了一个首项为$1$，末项为$100$，公差为$1$的等差数列。
对于等差数列，其求和公式为$S_n=\frac{n(a_1 + a_n)}{2}$（其中$S_n$表示前$n$项和，$a_1$表示首项，$a_n$表示末项，$n$表示项数）。
在这个数列中，$n = 100$，$a_1=1$，$a_n = 100$，将其代入公式可得：
$S_{100}=\frac{100×(1 + 100)}{2}$
$=\frac{100×101}{2}$
$= 50×101$
$= 5050$
使用计算器计算相对简单，但在这个场景下，利用等差数列求和公式计算更高效、准确，不需要用计算器逐步相加。
答案：$5050$；不打算；因为可以利用等差数列求和公式$\frac{n(a_1 + a_n)}{2}$来简便计算，其中$n = 100$，$a_1=1$，$a_n = 100$，代入可得$\frac{100×(1 + 100)}{2}=5050$，比用计算器逐步相加更简便。

4. 丁丁用计算器计算$9071-432$,并记录了操作过程。

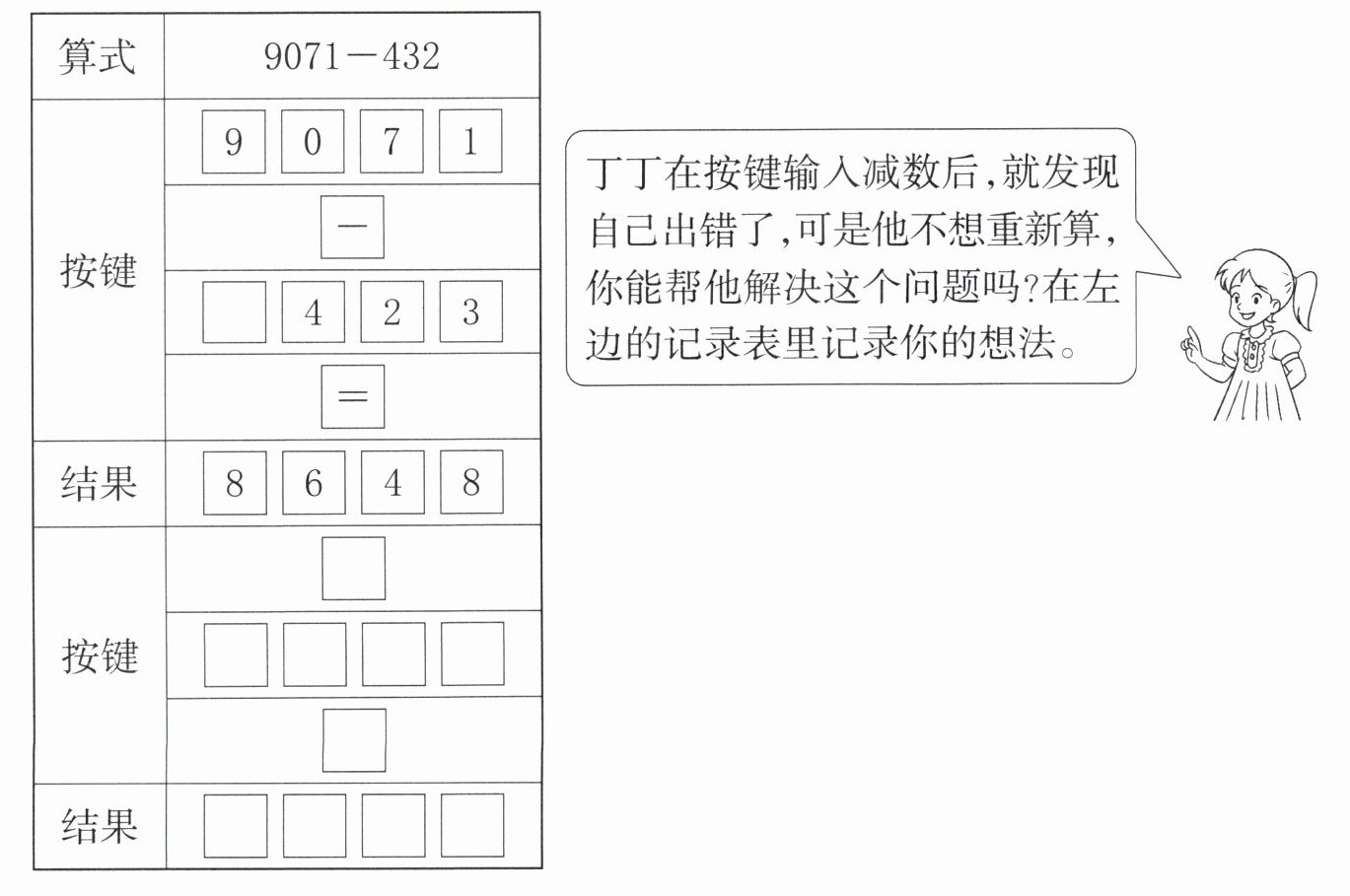
- 9 = 8639

答案： - 9 = 8639