《2025年课时提优计划作业本七年级数学上册苏科版基础强化版》

1. 《几何原本》是古希腊数学家所著的一部数学著作,共13卷,这本著作是现代数学的基础,在西方是仅次于《圣经》而流传最广的书籍,这位古希腊数学家是 ( )

A.利玛窦
B.高斯
C.李善兰
D.欧几里得

答案： D

2. 下列图形中,不属于“七巧板”中的图形的是 ( )

A.正方形
B.等边三角形
C.等腰直角三角形
D.平行四边形

答案： B

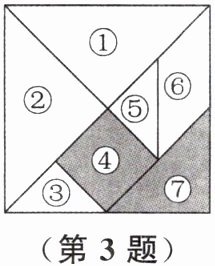
3. 如图是七巧板拼成的正方形,其中图形⑦和图形④共占正方形面积的______.(填分数)

答案： $\frac{1}{4}$ 解析:易知图形⑦与图形④的面积相等,图形④占大正方形的$1÷8=\frac{1}{8}$,故图形⑦和图形④共占大正方形的$\frac{1}{8}+\frac{1}{8}=\frac{2}{8}=\frac{1}{4}$.

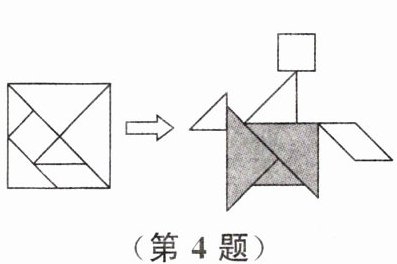
4. 如图,用边长为4 cm的正方形做了一套七巧板,拼成如图所示的一幅图案,则图中阴影部分的面积为$______cm^2.$

答案： 9 解析:如图,阴影部分面积是由①,②和④(或⑥)这三部分组成的.因为①和②是相同的等腰直角三角形,④和⑥也是相同的等腰直角三角形,所以阴影部分的面积为$\frac{1}{2}×4×2+\frac{1}{2}×4×2+\frac{1}{2}×2×1=9(cm^2)$.

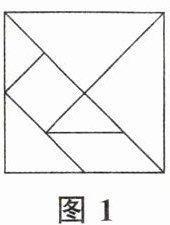
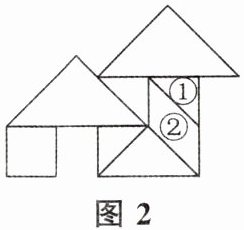
5. 如图,数学兴趣小组在综合与实践课上先用一张边长为8 cm的正方形纸片制作了一幅如图1所示的七巧板,再拼成如图2所示的作品,则图2中①和②的面积之和是 ( )


$A. 12 cm^2$
$B. 14 cm^2$
$C. 16 cm^2$
$D. 18 cm^2$

答案： A 解析:$8×8×\left(\frac{1}{8}+\frac{1}{16}\right)=12(cm^2)$,即图中①和②的面积之和是$12\ cm^2$.

6. 阅读课本材料数学实验室“七巧板”相关内容,解决下列问题.
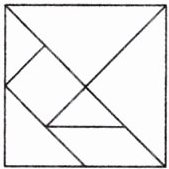
“七巧板”是我国古代劳动人民发明的一种益智玩具,由七块板组成,可以拼出各种各样的图形.已知一副七巧板是由一块正方形薄板分割而成,其中大三角形两块、小三角形两块、中三角形一块、正方形一块、平行四边形一块.
(1)若七巧板中小三角形的面积为a,求大三角形的面积.
(2)用七巧板中的三块板拼成一个等腰直角三角形,有几种不同的拼法？请简要说明.
(3)如图,用七巧板拼成了一个边长为8的大正方形,求图中平行四边形的面积.

答案：
(1)观察七巧板可知,大三角形的直角边长是小三角形直角边长的2倍.设小三角形的直角边长为$x$,则小三角形的面积$a=\frac{1}{2}\cdot x\cdot x=\frac{1}{2}x^2$,大三角形的直角边长为$2x$,则大三角形的面积$S=\frac{1}{2}\cdot(2x)\cdot(2x)=2x^2=4a$.
(2)有3种不同的拼法,如图所示.
(3)已知拼成的大正方形边长为8,则大正方形的面积为$8×8=64$.观察七巧板可知,平行四边形的面积是大正方形面积的$\frac{1}{8}$,则平行四边形的面积为$64×\frac{1}{8}=8$.