《2025年通城学典课时作业本五年级数学上册苏教版》

1. 根据运算规律,在□里填合适的字母或数。
(1)$2.5×(n×4)= n×(□×□)$
(2)$a - b - c= □-(□+□)$
(3)$a÷ b÷ c= □÷(□×□)$
(4)$x - 0.8x= (□-□)×□$

答案： 1.
(1) 2.5 4
(2) a b c
(3) a b c
(4) 1 0.8 x

2. 谨慎选择。
(1)下面各组中的两个式子结果一定相同的是( )。
A. $2a和a^2$
B. $x\cdot x和x^2$
C. $4 + 3m和7m$
D. $n× n× n和3n$
(2)(名校真题)一个小数,十位上的数字是$m$,十分位上的数字是$n$,这个小数为( )。
A. $m + n$
B. $mn$
C. $10m + 0.1n$
D. $10m + n$

答案： 2.
(1) B
(2) C

3. 仔细想,认真填。
(1)下图中的铅笔长( )cm。

(2)学校食堂有面粉3吨,计划每天用$a$千克,实际每天少用$b$千克,$3(a - b)$表示( ),用了30天,还剩下( )千克面粉。
(3)一个等腰三角形的其中一个底角是$a^{\circ}$,那么它的顶角是( )°；如果它的一条边长是$b$厘米,另一条边长是$2b$厘米,那么它的周长是( )厘米。

答案： 3.
(1) a-5
(2) 3天实际用的面粉质量 3000-30(a-b)
(3) 180-2a 5b

4. 邮票素有“国家名片”之称,方寸之间,包罗万象。聪聪爸爸是一位集邮爱好者,他的集邮册里,每页贴$a$行邮票,每行贴$b$枚,一共贴了8页。
(1)用含有字母的式子表示贴邮票的数量。
(2)如果$a = 6$,$b = 5$,那么聪聪爸爸一共贴了多少枚邮票？

答案： 4.
(1) 8ab枚
(2) 当a=6,b=5时,8ab=8×6×5=240 一共贴了240枚邮票

5. (数形结合)如图,一个长方形的长是$a$米,宽是$b$米。如果长和宽各增加3米。

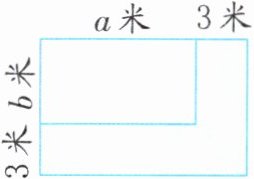
(1)用含有字母的式子表示面积增加了( )平方米。
(2)当$a = 9$,$b = 5$时,面积增加了多少平方米？
(3)明明提出了新的观点,他的说法正确吗？请写出你的想法。

答案： 5.
(1) 3a+3b+9
(2) 当a=9,b=5时,3a+3b+9=3×9+3×5+9=51 面积增加了51平方米
(3) 正确 因为由
(1)可知，长和宽无论是多少米，增加3米后，长方形增加的面积都是(3a+3b+9)平方米，而长方形的周长是2(a+b)米，由此可知a+b的值，从而求出长方形增加的面积

6. (探索规律)下面每个小长方形的长是$x$ cm,宽是$y$ cm。用含有字母的式子表示各个图形的周长。
( )cm
( )cm
( )cm
...
按上图的方式摆$n$层,此时图形的周长是( )cm。

答案：
6. 2(x+y) 4(x+y) 6(x+y) 2n(x+y) 解析:按题图中的方式摆长方形，第一幅图长是xcm,宽是ycm。第二、三幅图分别可以转化为如下长方形:(单位:cm) 　　 　　　 即第二幅图的长为2xcm,宽为2ycm;第三幅图的长为3xcm,宽为3ycm。摆n层，即第n幅图的长为nxcm，宽为nycm。再利用长方形的周长公式可以分别计算出各个图形的周长。