2025年美迪初中衔接暑假河北教育出版社数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年美迪初中衔接暑假河北教育出版社数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
[例1] 下列各式有意义时,求$x$的取值范围。
(1)$\sqrt{x + 2}$;(2)$\frac{1}{x - 1}$。
(1)$\sqrt{x + 2}$;(2)$\frac{1}{x - 1}$。
答案:
【解析】:本题考查分式与二次根式有意义的条件。对于二次根式,被开方数须为非负数;对于分式,分母不能为零。
(1)$\sqrt{x + 2}$是二次根式,要使其有意义,被开方数$x + 2$必须大于等于0,即解不等式$x + 2\geq0$。
(2)$\frac{1}{x - 1}$是分式,要使其有意义,分母$x - 1$不能等于0,即解等式$x - 1\neq0$。
【答案】:(1)$x\geq - 2$
(2)$x\neq1$
(1)$\sqrt{x + 2}$是二次根式,要使其有意义,被开方数$x + 2$必须大于等于0,即解不等式$x + 2\geq0$。
(2)$\frac{1}{x - 1}$是分式,要使其有意义,分母$x - 1$不能等于0,即解等式$x - 1\neq0$。
【答案】:(1)$x\geq - 2$
(2)$x\neq1$
对于(1)要使得$x + 2 \geq 0$,对于(2)要使得$x - 1 \neq 0$。
解:(1) 因为式子$\sqrt{x + 2}$有意义,所以$x + 2 \geq 0$,所以$x \geq -2$,所以$x的取值范围是x \geq -2$。
(2) 因为式子$\frac{1}{x - 1}$有意义,所以$x - 1 \neq 0$,所以$x \neq 1$,所以$x的取值范围是x \neq 1$。
[反思归纳] 分式有意义,则分式的分母不等于0;二次根式有意义,则二次根式的被开方式大于等于0。
解:(1) 因为式子$\sqrt{x + 2}$有意义,所以$x + 2 \geq 0$,所以$x \geq -2$,所以$x的取值范围是x \geq -2$。
(2) 因为式子$\frac{1}{x - 1}$有意义,所以$x - 1 \neq 0$,所以$x \neq 1$,所以$x的取值范围是x \neq 1$。
[反思归纳] 分式有意义,则分式的分母不等于0;二次根式有意义,则二次根式的被开方式大于等于0。
答案:
【解析】:本题考查分式和二次根式有意义的条件。对于二次根式$\sqrt{a}$,被开方数$a$必须是非负数,即$a\geq0$;对于分式$\frac{A}{B}$,分母$B$不能为$0$,即$B\neq0$。
(1) 式子$\sqrt{x + 2}$是二次根式,要使其有意义,被开方数$x + 2$需大于等于$0$,解这个不等式即可得到$x$的取值范围。
(2) 式子$\frac{1}{x - 1}$是分式,要使其有意义,分母$x - 1$需不等于$0$,解这个等式即可得到$x$的取值范围。
【答案】:
(1) $x \geq -2$
(2) $x \neq 1$
(1) 式子$\sqrt{x + 2}$是二次根式,要使其有意义,被开方数$x + 2$需大于等于$0$,解这个不等式即可得到$x$的取值范围。
(2) 式子$\frac{1}{x - 1}$是分式,要使其有意义,分母$x - 1$需不等于$0$,解这个等式即可得到$x$的取值范围。
【答案】:
(1) $x \geq -2$
(2) $x \neq 1$
[例2] 化简:$\frac{x}{x + \frac{1 - x}{x - \frac{1}{x}}}$。
答案:
【解析】:本题考查分式的化简,属于九年级数学分式章节内容。解题时需从最内层的分母开始逐步向外进行化简,遵循分式运算的基本法则,先算小括号内的式子,再依次向外计算。
【答案】:解:原式$=\frac{x}{x + \frac{1 - x}{\frac{x^2 - 1}{x}}}$
$=\frac{x}{x + (1 - x) \cdot \frac{x}{(x + 1)(x - 1)}}$
$=\frac{x}{x - \frac{x}{x + 1}}$
$=\frac{x}{\frac{x(x + 1) - x}{x + 1}}$
$=\frac{x}{\frac{x^2}{x + 1}}$
$=x \cdot \frac{x + 1}{x^2}$
$=\frac{x + 1}{x}$
【答案】:解:原式$=\frac{x}{x + \frac{1 - x}{\frac{x^2 - 1}{x}}}$
$=\frac{x}{x + (1 - x) \cdot \frac{x}{(x + 1)(x - 1)}}$
$=\frac{x}{x - \frac{x}{x + 1}}$
$=\frac{x}{\frac{x(x + 1) - x}{x + 1}}$
$=\frac{x}{\frac{x^2}{x + 1}}$
$=x \cdot \frac{x + 1}{x^2}$
$=\frac{x + 1}{x}$
从化简分母中的分式$x + \frac{1 - x}{x - \frac{1}{x}}$入手,最后化成最简约分数。
答案:
解:方法一:原式$= \frac{x}{x + \frac{1 - x}{\frac{x^2 - 1}{x}}}$
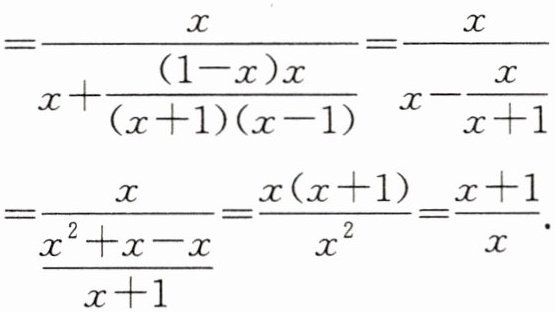
$= \frac{x}{x + \frac{(1 - x)x}{(x + 1)(x - 1)}} = \frac{x}{x - \frac{x}{x + 1}}$
$= \frac{x}{\frac{x^2 + x - x}{x + 1}} = \frac{x(x + 1)}{x^2} = \frac{x + 1}{x}$。
方法二:原式$= \frac{x}{x + \frac{(1 - x)x}{(x - \frac{1}{x})x}}$
$= \frac{x}{x + \frac{(1 - x)x}{x^2 - 1}} = \frac{x}{x - \frac{x}{x + 1}}$
$= \frac{x(x + 1)}{x^2 + x - x} = \frac{x + 1}{x}$。
[反思归纳] 繁分式化简,一般可以从最内部的分式入手,采取通分的方式逐步脱掉繁分式,或利用分式的基本性质$\frac{A}{B} = \frac{A × M}{B × M} = \frac{A ÷ M}{B ÷ M}(M \neq 0)$进行化简。一般根据题目特点,综合使用两种方法。
解:方法一:原式$= \frac{x}{x + \frac{1 - x}{\frac{x^2 - 1}{x}}}$
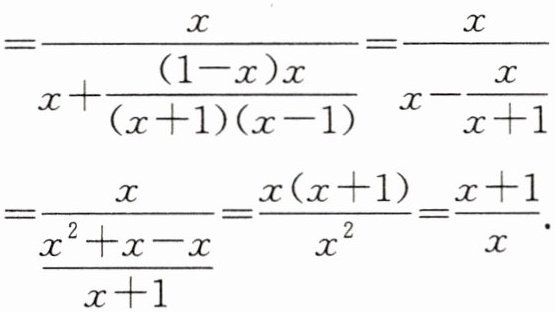
$= \frac{x}{x + \frac{(1 - x)x}{(x + 1)(x - 1)}} = \frac{x}{x - \frac{x}{x + 1}}$
$= \frac{x}{\frac{x^2 + x - x}{x + 1}} = \frac{x(x + 1)}{x^2} = \frac{x + 1}{x}$。
方法二:原式$= \frac{x}{x + \frac{(1 - x)x}{(x - \frac{1}{x})x}}$
$= \frac{x}{x + \frac{(1 - x)x}{x^2 - 1}} = \frac{x}{x - \frac{x}{x + 1}}$
$= \frac{x(x + 1)}{x^2 + x - x} = \frac{x + 1}{x}$。
[反思归纳] 繁分式化简,一般可以从最内部的分式入手,采取通分的方式逐步脱掉繁分式,或利用分式的基本性质$\frac{A}{B} = \frac{A × M}{B × M} = \frac{A ÷ M}{B ÷ M}(M \neq 0)$进行化简。一般根据题目特点,综合使用两种方法。
[例3] 化简:
(1)$\sqrt{7 - 4\sqrt{3}} + \sqrt{4 - 2\sqrt{3}}$;
(2)$\frac{\sqrt{a}}{a - \sqrt{ab}} + \frac{\sqrt{a}}{a + \sqrt{ab}}$。
(1)$\sqrt{7 - 4\sqrt{3}} + \sqrt{4 - 2\sqrt{3}}$;
(2)$\frac{\sqrt{a}}{a - \sqrt{ab}} + \frac{\sqrt{a}}{a + \sqrt{ab}}$。
答案:
【解析】:
(1) 对于$\sqrt{7 - 4\sqrt{3}} + \sqrt{4 - 2\sqrt{3}}$,需将根号下的式子化为完全平方形式。观察$7 - 4\sqrt{3}$,可拆分为$(\sqrt{3})^2 - 4\sqrt{3} + 2^2 = (\sqrt{3} - 2)^2$,因为$2 > \sqrt{3}$,所以开方得$2 - \sqrt{3}$;$4 - 2\sqrt{3}$可拆分为$(\sqrt{3})^2 - 2\sqrt{3} + 1^2 = (\sqrt{3} - 1)^2$,开方得$\sqrt{3} - 1$,两者相加即可。
(2) 对于$\frac{\sqrt{a}}{a - \sqrt{ab}} + \frac{\sqrt{a}}{a + \sqrt{ab}}$,先对分母进行因式分解,提取公因式$\sqrt{a}$,得到$\sqrt{a}(\sqrt{a} - \sqrt{b})$和$\sqrt{a}(\sqrt{a} + \sqrt{b})$,然后约分化简,再通分相加,最后分母有理化。
【答案】:
(1) 解:原式$=\sqrt{(\sqrt{3}-2)^2} + \sqrt{(\sqrt{3}-1)^2}$
$=2 - \sqrt{3} + \sqrt{3} - 1$
$=1$
(2) 解:原式$=\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} - \sqrt{b})} + \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} + \sqrt{b})}$
$=\frac{1}{\sqrt{a} - \sqrt{b}} + \frac{1}{\sqrt{a} + \sqrt{b}}$
$=\frac{\sqrt{a} + \sqrt{b} + \sqrt{a} - \sqrt{b}}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})}$
$=\frac{2\sqrt{a}}{a - b}$
(1) 对于$\sqrt{7 - 4\sqrt{3}} + \sqrt{4 - 2\sqrt{3}}$,需将根号下的式子化为完全平方形式。观察$7 - 4\sqrt{3}$,可拆分为$(\sqrt{3})^2 - 4\sqrt{3} + 2^2 = (\sqrt{3} - 2)^2$,因为$2 > \sqrt{3}$,所以开方得$2 - \sqrt{3}$;$4 - 2\sqrt{3}$可拆分为$(\sqrt{3})^2 - 2\sqrt{3} + 1^2 = (\sqrt{3} - 1)^2$,开方得$\sqrt{3} - 1$,两者相加即可。
(2) 对于$\frac{\sqrt{a}}{a - \sqrt{ab}} + \frac{\sqrt{a}}{a + \sqrt{ab}}$,先对分母进行因式分解,提取公因式$\sqrt{a}$,得到$\sqrt{a}(\sqrt{a} - \sqrt{b})$和$\sqrt{a}(\sqrt{a} + \sqrt{b})$,然后约分化简,再通分相加,最后分母有理化。
【答案】:
(1) 解:原式$=\sqrt{(\sqrt{3}-2)^2} + \sqrt{(\sqrt{3}-1)^2}$
$=2 - \sqrt{3} + \sqrt{3} - 1$
$=1$
(2) 解:原式$=\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} - \sqrt{b})} + \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} + \sqrt{b})}$
$=\frac{1}{\sqrt{a} - \sqrt{b}} + \frac{1}{\sqrt{a} + \sqrt{b}}$
$=\frac{\sqrt{a} + \sqrt{b} + \sqrt{a} - \sqrt{b}}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})}$
$=\frac{2\sqrt{a}}{a - b}$
(1) 将$7 - 4\sqrt{3}和4 - 2\sqrt{3}$改写成完全平方的形式,脱去最外层根号,进行化简;(2) 先把两个分式化简,然后通分。
解:(1) 原式$= \sqrt{(2 - \sqrt{3})^2} + \sqrt{(\sqrt{3} - 1)^2} = |2 - \sqrt{3}| + |\sqrt{3} - 1| = 2 - \sqrt{3} + \sqrt{3} - 1 = 1$。
(2) 原式$= \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} - \sqrt{b})} + \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} + \sqrt{b})} = \frac{1}{\sqrt{a} - \sqrt{b}} + \frac{1}{\sqrt{a} + \sqrt{b}} = \frac{(\sqrt{a} + \sqrt{b}) + (\sqrt{a} - \sqrt{b})}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})} = \frac{2\sqrt{a}}{a - b}$。
[反思归纳] 根号中有根号的化简一般是构造完全平方式求解,含有根式的分式化简,一般可以通过约掉公因式、通分化简,或分母有理化化简。
解:(1) 原式$= \sqrt{(2 - \sqrt{3})^2} + \sqrt{(\sqrt{3} - 1)^2} = |2 - \sqrt{3}| + |\sqrt{3} - 1| = 2 - \sqrt{3} + \sqrt{3} - 1 = 1$。
(2) 原式$= \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} - \sqrt{b})} + \frac{\sqrt{a}}{\sqrt{a}(\sqrt{a} + \sqrt{b})} = \frac{1}{\sqrt{a} - \sqrt{b}} + \frac{1}{\sqrt{a} + \sqrt{b}} = \frac{(\sqrt{a} + \sqrt{b}) + (\sqrt{a} - \sqrt{b})}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})} = \frac{2\sqrt{a}}{a - b}$。
[反思归纳] 根号中有根号的化简一般是构造完全平方式求解,含有根式的分式化简,一般可以通过约掉公因式、通分化简,或分母有理化化简。
答案:
【解析】:
(1) 本题考查二次根式的化简,关键是将被开方数构造成完全平方的形式。对于形如$\sqrt{m - n\sqrt{k}}$的二次根式,可尝试将其化为$\sqrt{(\sqrt{a} - \sqrt{b})^2}$的形式,其中$a + b = m$,$2\sqrt{ab} = n\sqrt{k}$。对于$\sqrt{7 - 4\sqrt{3}}$,通过计算可知$a = 4$,$b = 3$时满足条件,即$7 - 4\sqrt{3}=(\sqrt{4}-\sqrt{3})^2=(2 - \sqrt{3})^2$;同理,$4 - 2\sqrt{3}=(\sqrt{3}-1)^2$。然后根据二次根式的性质$\sqrt{a^2}=|a|$,因为$2 - \sqrt{3}>0$,$\sqrt{3}-1>0$,所以绝对值符号可直接去掉,进而化简得出结果。
(2) 本题考查分式的化简与通分,涉及分母有理化知识。首先观察分式的分子分母,发现分子分母有公因式$\sqrt{a}$,先约分化简,得到$\frac{1}{\sqrt{a}-\sqrt{b}}+\frac{1}{\sqrt{a}+\sqrt{b}}$。然后找到两个分式的最简公分母为$(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$,通分后将分子相加,再利用平方差公式$(\sqrt{a})^2 - (\sqrt{b})^2 = a - b$化简分母,最后合并分子同类项得出结果。
【答案】:
(1) $\sqrt{7 - 4\sqrt{3}}+\sqrt{4 - 2\sqrt{3}}$
$=\sqrt{(2 - \sqrt{3})^2}+\sqrt{(\sqrt{3}-1)^2}$
$=|2 - \sqrt{3}|+|\sqrt{3}-1|$
$=2 - \sqrt{3}+\sqrt{3}-1$
$=1$
(2) $\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a}-\sqrt{b})}+\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a}+\sqrt{b})}$
$=\frac{1}{\sqrt{a}-\sqrt{b}}+\frac{1}{\sqrt{a}+\sqrt{b}}$
$=\frac{(\sqrt{a}+\sqrt{b})+(\sqrt{a}-\sqrt{b})}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}$
$=\frac{2\sqrt{a}}{a - b}$
(1) 本题考查二次根式的化简,关键是将被开方数构造成完全平方的形式。对于形如$\sqrt{m - n\sqrt{k}}$的二次根式,可尝试将其化为$\sqrt{(\sqrt{a} - \sqrt{b})^2}$的形式,其中$a + b = m$,$2\sqrt{ab} = n\sqrt{k}$。对于$\sqrt{7 - 4\sqrt{3}}$,通过计算可知$a = 4$,$b = 3$时满足条件,即$7 - 4\sqrt{3}=(\sqrt{4}-\sqrt{3})^2=(2 - \sqrt{3})^2$;同理,$4 - 2\sqrt{3}=(\sqrt{3}-1)^2$。然后根据二次根式的性质$\sqrt{a^2}=|a|$,因为$2 - \sqrt{3}>0$,$\sqrt{3}-1>0$,所以绝对值符号可直接去掉,进而化简得出结果。
(2) 本题考查分式的化简与通分,涉及分母有理化知识。首先观察分式的分子分母,发现分子分母有公因式$\sqrt{a}$,先约分化简,得到$\frac{1}{\sqrt{a}-\sqrt{b}}+\frac{1}{\sqrt{a}+\sqrt{b}}$。然后找到两个分式的最简公分母为$(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})$,通分后将分子相加,再利用平方差公式$(\sqrt{a})^2 - (\sqrt{b})^2 = a - b$化简分母,最后合并分子同类项得出结果。
【答案】:
(1) $\sqrt{7 - 4\sqrt{3}}+\sqrt{4 - 2\sqrt{3}}$
$=\sqrt{(2 - \sqrt{3})^2}+\sqrt{(\sqrt{3}-1)^2}$
$=|2 - \sqrt{3}|+|\sqrt{3}-1|$
$=2 - \sqrt{3}+\sqrt{3}-1$
$=1$
(2) $\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a}-\sqrt{b})}+\frac{\sqrt{a}}{\sqrt{a}(\sqrt{a}+\sqrt{b})}$
$=\frac{1}{\sqrt{a}-\sqrt{b}}+\frac{1}{\sqrt{a}+\sqrt{b}}$
$=\frac{(\sqrt{a}+\sqrt{b})+(\sqrt{a}-\sqrt{b})}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}$
$=\frac{2\sqrt{a}}{a - b}$
查看更多完整答案,请扫码查看


