2025年美迪初中衔接暑假河北教育出版社数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年美迪初中衔接暑假河北教育出版社数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
[例 1] 作出二次函数 $ f ( x ) = - x ^ { 2 } + 2 x + 3 $ 的图象,并根据图象解答下列问题.
(1)比较 $ f ( 0 ) $,$ f ( 1 ) $,$ f ( 3 ) $ 的大小;
(2)若 $ x _ { 1 } < x _ { 2 } < 1 $,比较 $ f ( x _ { 1 } ) $ 与 $ f ( x _ { 2 } ) $ 的大小;
(3)求函数 $ f ( x ) $ 的值域.
思维启迪 作出二次函数 $ f ( x ) = - x ^ { 2 } + 2 x + 3 $ 的图象,数形结合求解.
解:(1)因为 $ f ( x ) = - x ^ { 2 } + 2 x + 3 $,
所以 $ f ( 0 ) = 3 $,$ f ( 1 ) = 4 $,$ f ( 3 ) = 0 $,
所以 $ f ( 1 ) > f ( 0 ) > f ( 3 ) $.
(2)$ f ( x ) = - x ^ { 2 } + 2 x + 3 = - ( x - 1 ) ^ { 2 } + 4 $ 的图象如图所示.
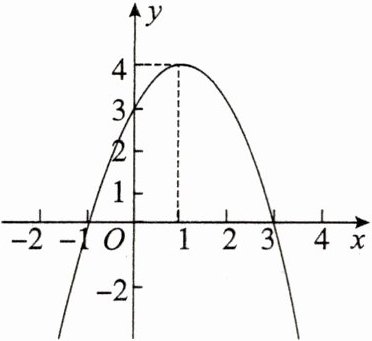
由图象可以看出,当 $ x _ { 1 } < x _ { 2 } < 1 $ 时,函数 $ f ( x ) $ 的值随着 $ x $ 的增大而增大,
所以 $ f ( x _ { 1 } ) < f ( x _ { 2 } ) $.
(3)由图象可以看出,函数 $ f ( x ) $ 的值域为 $ ( - \infty, 4 ] $.
[反思归纳](1)若给出的二次函数的形式是一般式,可将一般式进行配方,化为顶点式,可以直接选出关键点,减少了选点的盲目性,使得画图更简便、图象更精准;(2)根据图象的直观性求解各种问题,体现了“数形结合”思想的应用.
(1)比较 $ f ( 0 ) $,$ f ( 1 ) $,$ f ( 3 ) $ 的大小;
(2)若 $ x _ { 1 } < x _ { 2 } < 1 $,比较 $ f ( x _ { 1 } ) $ 与 $ f ( x _ { 2 } ) $ 的大小;
(3)求函数 $ f ( x ) $ 的值域.
思维启迪 作出二次函数 $ f ( x ) = - x ^ { 2 } + 2 x + 3 $ 的图象,数形结合求解.
解:(1)因为 $ f ( x ) = - x ^ { 2 } + 2 x + 3 $,
所以 $ f ( 0 ) = 3 $,$ f ( 1 ) = 4 $,$ f ( 3 ) = 0 $,
所以 $ f ( 1 ) > f ( 0 ) > f ( 3 ) $.
(2)$ f ( x ) = - x ^ { 2 } + 2 x + 3 = - ( x - 1 ) ^ { 2 } + 4 $ 的图象如图所示.

由图象可以看出,当 $ x _ { 1 } < x _ { 2 } < 1 $ 时,函数 $ f ( x ) $ 的值随着 $ x $ 的增大而增大,
所以 $ f ( x _ { 1 } ) < f ( x _ { 2 } ) $.
(3)由图象可以看出,函数 $ f ( x ) $ 的值域为 $ ( - \infty, 4 ] $.
[反思归纳](1)若给出的二次函数的形式是一般式,可将一般式进行配方,化为顶点式,可以直接选出关键点,减少了选点的盲目性,使得画图更简便、图象更精准;(2)根据图象的直观性求解各种问题,体现了“数形结合”思想的应用.
答案:
【解析】:本题考查二次函数的图象与性质。首先将二次函数化为顶点式,确定顶点坐标、对称轴等关键信息,然后作出函数图象,再根据图象解决比较函数值大小、判断函数单调性及求函数值域等问题。
1. 对于比较$f(0)$,$f(1)$,$f(3)$的大小,可直接代入函数解析式计算出各函数值,再进行比较。
2. 比较当$x_1<x_2<1$时$f(x_1)$与$f(x_2)$的大小,需根据二次函数的单调性,由函数图象开口方向和对称轴判断在给定区间上的增减性。
3. 求函数的值域,结合二次函数的顶点式及开口方向确定最大值,进而得出值域。
【答案】:
解:作出二次函数$f(x) = -x^2 + 2x + 3$的图象,图略。
(1) 因为$f(x) = -x^2 + 2x + 3$,
所以$f(0) = -0^2 + 2×0 + 3 = 3$,
$f(1) = -1^2 + 2×1 + 3 = 4$,
$f(3) = -3^2 + 2×3 + 3 = 0$,
所以$f(1)>f(0)>f(3)$。
(2) $f(x) = -x^2 + 2x + 3 = -(x - 1)^2 + 4$,
其图象开口向下,对称轴为直线$x = 1$,
由图象可知,当$x<1$时,函数$f(x)$的值随着$x$的增大而增大,
因为$x_1<x_2<1$,
所以$f(x_1)<f(x_2)$。
(3) 由$f(x) = -(x - 1)^2 + 4$可知,函数图象开口向下,顶点坐标为$(1, 4)$,
所以函数$f(x)$的最大值为$4$,
则函数$f(x)$的值域为$(-\infty, 4]$。
1. 对于比较$f(0)$,$f(1)$,$f(3)$的大小,可直接代入函数解析式计算出各函数值,再进行比较。
2. 比较当$x_1<x_2<1$时$f(x_1)$与$f(x_2)$的大小,需根据二次函数的单调性,由函数图象开口方向和对称轴判断在给定区间上的增减性。
3. 求函数的值域,结合二次函数的顶点式及开口方向确定最大值,进而得出值域。
【答案】:
解:作出二次函数$f(x) = -x^2 + 2x + 3$的图象,图略。
(1) 因为$f(x) = -x^2 + 2x + 3$,
所以$f(0) = -0^2 + 2×0 + 3 = 3$,
$f(1) = -1^2 + 2×1 + 3 = 4$,
$f(3) = -3^2 + 2×3 + 3 = 0$,
所以$f(1)>f(0)>f(3)$。
(2) $f(x) = -x^2 + 2x + 3 = -(x - 1)^2 + 4$,
其图象开口向下,对称轴为直线$x = 1$,
由图象可知,当$x<1$时,函数$f(x)$的值随着$x$的增大而增大,
因为$x_1<x_2<1$,
所以$f(x_1)<f(x_2)$。
(3) 由$f(x) = -(x - 1)^2 + 4$可知,函数图象开口向下,顶点坐标为$(1, 4)$,
所以函数$f(x)$的最大值为$4$,
则函数$f(x)$的值域为$(-\infty, 4]$。
查看更多完整答案,请扫码查看


