《2025年美迪初中衔接暑假河北教育出版社数学人教版》

3. (对应题型三)(1)已知$x＞0,y＞0,x+2y= 1$,求证:$(1+\frac {2}{x})(1+\frac {1}{y})≥25$;
(2)已知$a＞0,b＞0,c＞0$,且$a+b+c= 1$,求证:$\frac {1}{a}+\frac {1}{b}+\frac {1}{c}≥9$.

答案： 【解析】：本题考查基本不等式的应用。（1）题已知$x＞0,y＞0$且$x + 2y=1$，要证明$(1+\frac{2}{x})(1+\frac{1}{y})≥25$，可将$1$用$x + 2y$替换，展开后利用基本不等式$a + b≥2\sqrt{ab}$（$a,b＞0$，当且仅当$a = b$时取等号）进行证明；（2）题已知$a＞0,b＞0,c＞0$且$a + b + c=1$，证明$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≥9$，同样将$1$用$a + b + c$替换，然后展开，再利用基本不等式证明。
【答案】：证明：
(1)
∵$x＞0,y＞0,x + 2y=1$
∴$(1+\frac{2}{x})(1+\frac{1}{y})=(1+\frac{2}{x})(1+\frac{1}{y})$
$=1+\frac{1}{y}+\frac{2}{x}+\frac{2}{xy}$
$=1+\frac{x + 2y}{xy}+\frac{2}{xy}$（将$1$用$x + 2y$替换$\frac{x + 2y}{xy}$）
∵$x + 2y=1$
∴$=1+\frac{1}{xy}+\frac{2}{xy}=1+\frac{3}{xy}$
又
∵$x + 2y=1≥2\sqrt{2xy}$（基本不等式，$x＞0,y＞0$）
∴$\sqrt{2xy}≤\frac{1}{2}$，两边平方得$2xy≤\frac{1}{4}$，即$xy≤\frac{1}{8}$，则$\frac{1}{xy}≥8$
∴$1+\frac{3}{xy}≥1 + 3×8=25$
当且仅当$x = 2y$，结合$x + 2y=1$，解得$x=\frac{1}{2},y=\frac{1}{4}$时取等号
∴$(1+\frac{2}{x})(1+\frac{1}{y})≥25$
(2)
∵$a＞0,b＞0,c＞0,a + b + c=1$
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a + b + c}{a}+\frac{a + b + c}{b}+\frac{a + b + c}{c}$（将$1$用$a + b + c$替换）
$=1+\frac{b}{a}+\frac{c}{a}+1+\frac{a}{b}+\frac{c}{b}+1+\frac{a}{c}+\frac{b}{c}$
$=3+(\frac{b}{a}+\frac{a}{b})+(\frac{c}{a}+\frac{a}{c})+(\frac{c}{b}+\frac{b}{c})$
∵$\frac{b}{a}+\frac{a}{b}≥2\sqrt{\frac{b}{a}×\frac{a}{b}}=2$（基本不等式，$a,b＞0$），同理$\frac{c}{a}+\frac{a}{c}≥2$，$\frac{c}{b}+\frac{b}{c}≥2$
∴$3 + 2 + 2 + 2=9$
当且仅当$a = b = c=\frac{1}{3}$时取等号
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≥9$

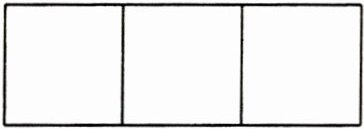
4. (对应题型四)某工厂拟建一座平面图为矩形且面积为400平方米的三级污水处理池,平面图如图所示.已知处理池外圈建造单价为每米200元,中间两条隔墙建造单价每米250元,池底建造单价为每平方米80元(隔墙与池底的厚度忽略不计,且池无盖).试设计处理池的长与宽,使得总造价最低,并求出最低造价.

答案： 【解析】：本题考查基本不等式在实际问题中的应用。首先，根据矩形面积设出长和宽，然后分别表示出外圈周长、隔墙长度，进而得出总造价的表达式，最后利用基本不等式求最小值。
设矩形污水处理池的长为x米，宽为y米，已知面积为400平方米，所以xy = 400，即$y=\frac{400}{x}。$
外圈周长为2(x + y)，中间两条隔墙与宽平行，长度均为y，所以隔墙总长度为2y。
总造价C包括外圈造价、隔墙造价和池底造价。外圈造价为200×2(x + y)，隔墙造价为250×2y，池底造价为80×400。
则C=200×2(x + y)+250×2y + 80×400，化简得：
$\begin{aligned}C&=400(x + y)+500y + 32000\\&=400x + 400y + 500y + 32000\\&=400x + 900y + 32000\end{aligned}$
将$y=\frac{400}{x}$代入上式：
$C = 400x + 900×\frac{400}{x}+32000 = 400x+\frac{360000}{x}+32000$
根据基本不等式$a + b\geq2\sqrt{ab}（a,b＞0，$当且仅当a = b时取等号），对于$400x+\frac{360000}{x}，$a = 400x，$b=\frac{360000}{x}，$则：
$400x+\frac{360000}{x}\geq2\sqrt{400x×\frac{360000}{x}} = 2\sqrt{400×360000}=2×12000 = 24000$
当且仅当$400x=\frac{360000}{x}$时取等号，解方程$400x=\frac{360000}{x}$：
$400x^2 = 360000\Rightarrow x^2=900\Rightarrow x = 30（x＞0）$
此时$y=\frac{400}{x}=\frac{400}{30}=\frac{40}{3}。$所以最低总造价C = 24000 + 32000=56000元。【答案】：设计处理池的长为30米，宽为$\frac{40}{3}$米时，总造价最低，最低造价为56000元。