《2025年美迪初中衔接暑假河北教育出版社数学人教版》

1. 若$(x^{2}+mx+n)(x - 1) = x^{3} - 1$,则$m + n = $(D)
A.0
B.1
C.-1
D.2

答案： 【解析】：本题考查多项式乘法与因式分解的应用。首先，已知等式左边是两个多项式相乘，右边是$x^3 - 1$，而$x^3 - 1$可以利用立方差公式分解为$(x - 1)(x^2 + x + 1)$。将分解后的式子与左边对比，即可得出$m$和$n$的值，进而求出$m + n$。
因为$x^3 - 1=(x - 1)(x^2 + x + 1)$，又已知$(x^2 + mx + n)(x - 1)=x^3 - 1$，所以$(x^2 + mx + n)(x - 1)=(x - 1)(x^2 + x + 1)$。由于等式两边对应项系数相等，可得$m = 1$，$n = 1$，则$m + n=1 + 1 = 2$。
【答案】：D

2. 使得分式$\frac{1}{1 + \frac{1}{x}}有意义的x$的取值范围是(C)
A.$x \neq 0$
B.$x \neq - 1$
C.$x \neq - 1且x \neq 0$
D.$x \neq 1且x \neq 0$

答案： 【解析】：要使分式$\frac{1}{1 + \frac{1}{x}}$有意义，需保证分母不为零。该分式分母包含两部分，一是最外层分母$1+\frac{1}{x}$，二是内层分式$\frac{1}{x}$的分母$x$。首先，内层分式$\frac{1}{x}$有意义的条件是$x\neq0$；其次，外层分母$1+\frac{1}{x}$不能为零，即$1+\frac{1}{x}\neq0$，解这个不等式：$\frac{1}{x}\neq - 1$，可得$x\neq - 1$。综上，$x$需同时满足$x\neq0$且$x\neq - 1$。
【答案】：C

3. 不等式$|4x - 1| ＞ 4$的解是(A)
A.$x ＞ \frac{5}{4}或x ＜ - \frac{3}{4}$
B.$- \frac{3}{4} ＜ x ＜ \frac{5}{4}$
C.$x ＜ - \frac{3}{4}$
D.$x ＞ \frac{5}{4}$

答案： 【解析】：本题考查绝对值不等式的解法。对于不等式$|4x - 1| ＞ 4$，根据绝对值的性质，绝对值大于一个正数的数，其值在这个正数的两侧，即$4x - 1 ＞ 4$或$4x - 1 ＜ -4$。分别解这两个不等式，第一个不等式$4x - 1 ＞ 4$，移项可得$4x ＞ 5$，解得$x ＞ \frac{5}{4}$；第二个不等式$4x - 1 ＜ -4$，移项可得$4x ＜ -3$，解得$x ＜ -\frac{3}{4}$。所以不等式的解为$x ＞ \frac{5}{4}$或$x ＜ -\frac{3}{4}$。
【答案】：A

4. 在$\triangle ABC$中,$AD平分\angle BAC$,且$AB = 2$,$AC = 1$,则$S_{\triangle ABC}:S_{\triangle ADC} = $(D)
A.$1:2$
B.$2:1$
C.$1:3$
D.$3:1$

答案： 【解析】：本题考查三角形角平分线的性质及三角形面积公式。角平分线上的点到角两边的距离相等。设AD平分∠BAC，过点D分别作AB、AC的垂线，垂足为E、F，则DE=DF。根据三角形面积公式$S=\frac{1}{2}ah$，可得$S_{\triangle ABD}=\frac{1}{2}AB× DE$，$S_{\triangle ADC}=\frac{1}{2}AC× DF$。因为DE=DF，所以$S_{\triangle ABD}:S_{\triangle ADC}=AB:AC=2:1$。又因为$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ADC}$，所以$S_{\triangle ABC}:S_{\triangle ADC}=(2+1):1=3:1$。
【答案】：D

5. (多选)下列因式分解正确的有(BC)
A.$x^{2} - 7x - 30 = (x - 3)(x + 10)$
B.$9x^{2} - 30x + 25 = (3x - 5)^{2}$
C.$6x^{2} - 13x + 5 = (2x - 1)(3x - 5)$
D.$21x^{2} - 31x - 22 = (3x - 2)(7x + 11)$

答案： 【解析】：本题考查因式分解的知识点，需要对每个选项中的多项式进行因式分解验证。
选项A：将$(x - 3)(x + 10)$展开得$x^2 + 10x - 3x - 30 = x^2 + 7x - 30$，与原式$x^2 - 7x - 30$不符，所以A错误。
选项B：$9x^2 - 30x + 25$是完全平方形式，$(3x - 5)^2 = 9x^2 - 30x + 25$，所以B正确。
选项C：将$(2x - 1)(3x - 5)$展开得$6x^2 - 10x - 3x + 5 = 6x^2 - 13x + 5$，与原式一致，所以C正确。
选项D：将$(3x - 2)(7x + 11)$展开得$21x^2 + 33x - 14x - 22 = 21x^2 + 19x - 22$，与原式$21x^2 - 31x - 22$不符，所以D错误。
【答案】：BC

6. (多选)已知$a + \frac{1}{a} = 3$,则下列选项正确的有(ABC)
A.$a^{2} + \frac{1}{a^{2}} = 7$
B.$(a - \frac{1}{a})^{2} = 5$
C.$(\sqrt{a} - \frac{1}{\sqrt{a}})^{2} = 1$
D.$\sqrt{a} + \frac{1}{\sqrt{a}} = \pm \sqrt{5}$

答案： 【解析】：本题考查了完全平方公式的应用。已知$a + \frac{1}{a} = 3$，需要对各选项进行判断。
对于选项A：将$a + \frac{1}{a} = 3$两边平方，根据完全平方公式$(m + n)^2 = m^2 + 2mn + n^2$，可得$(a + \frac{1}{a})^2 = a^2 + 2 × a × \frac{1}{a} + \frac{1}{a^2} = a^2 + 2 + \frac{1}{a^2}$，即$3^2 = a^2 + 2 + \frac{1}{a^2}$，$9 = a^2 + \frac{1}{a^2} + 2$，所以$a^2 + \frac{1}{a^2} = 9 - 2 = 7$，选项A正确。
对于选项B：$(a - \frac{1}{a})^2 = a^2 - 2 × a × \frac{1}{a} + \frac{1}{a^2} = a^2 - 2 + \frac{1}{a^2}$，由选项A知$a^2 + \frac{1}{a^2} = 7$，所以$(a - \frac{1}{a})^2 = 7 - 2 = 5$，选项B正确。
对于选项C：$(\sqrt{a} - \frac{1}{\sqrt{a}})^2 = (\sqrt{a})^2 - 2 × \sqrt{a} × \frac{1}{\sqrt{a}} + (\frac{1}{\sqrt{a}})^2 = a - 2 + \frac{1}{a}$，因为$a + \frac{1}{a} = 3$，所以$(\sqrt{a} - \frac{1}{\sqrt{a}})^2 = 3 - 2 = 1$，选项C正确。
对于选项D：设$\sqrt{a} + \frac{1}{\sqrt{a}} = t$（$t ＞ 0$，因为$\sqrt{a}$有意义则$a ＞ 0$，所以$\sqrt{a} + \frac{1}{\sqrt{a}} ＞ 0$），两边平方得$(\sqrt{a} + \frac{1}{\sqrt{a}})^2 = a + 2 + \frac{1}{a}$，即$t^2 = 3 + 2 = 5$，所以$t = \sqrt{5}$，故$\sqrt{a} + \frac{1}{\sqrt{a}} = \sqrt{5}$，选项D错误。
综上，正确的选项为A、B、C。
【答案】：ABC

7. 若$2 ＜ a ＜ 3$,则代数式$|a - 3| + |2 - a|$的值为______1。

答案： 【解析】：本题考查绝对值的化简。因为$2 ＜ a ＜ 3$，所以$a - 3 ＜ 0$，$2 - a ＜ 0$。根据绝对值的性质，负数的绝对值是它的相反数，可得$|a - 3| = 3 - a$，$|2 - a| = a - 2$。则原式$= 3 - a + a - 2 = 1$。
【答案】：1

8. 已知$x^{2} + x - 1 = 0$,则$x^{3} - \frac{1}{x^{3}} = $-4。

答案： 【解析】：本题考查了一元二次方程的变形及代数式的化简求值。首先，由已知方程$x^{2} + x - 1 = 0$，因为$x\neq0$（若$x=0$，方程不成立），两边同时除以$x$可得$x + 1 - \frac{1}{x} = 0$，即$x - \frac{1}{x}=-1$。然后，对$x - \frac{1}{x}=-1$两边平方，得$(x - \frac{1}{x})^{2}=1$，展开可得$x^{2}-2+\frac{1}{x^{2}}=1$，所以$x^{2}+\frac{1}{x^{2}}=3$。最后，根据立方差公式$x^{3}-\frac{1}{x^{3}}=(x - \frac{1}{x})(x^{2}+1+\frac{1}{x^{2}})$，将$x - \frac{1}{x}=-1$和$x^{2}+\frac{1}{x^{2}}=3$代入，可得$x^{3}-\frac{1}{x^{3}}=-1×(3 + 1)=-4$。
【答案】：-4

9. 已知关于$x的方程x^{2} - 2(k - 1)x + k^{2} = 0有两个实数根x_{1}$,$x_{2}$。
(1)求实数$k$的取值范围；
(2)是否存在实数$k$,使得$x_{1} + x_{2} = 1 - x_{1}x_{2}$成立？若存在,求出$k$的值；若不存在,请说明理由。

答案： 【解析】：
(1)因为方程有两个实数根，所以判别式△≥0。对于一元二次方程$ax^2 + bx + c = 0$，判别式$\Delta = b^2 - 4ac$。在方程$x^2 - 2(k - 1)x + k^2 = 0$中，$a = 1$，$b = -2(k - 1)$，$c = k^2$，代入判别式可得$\Delta = [-2(k - 1)]^2 - 4×1×k^2$，化简后解不等式即可求出$k$的取值范围。
(2)根据韦达定理，在一元二次方程$ax^2 + bx + c = 0$中，两根之和$x_1 + x_2 = -\frac{b}{a}$，两根之积$x_1x_2 = \frac{c}{a}$。所以可表示出$x_1 + x_2$和$x_1x_2$，代入$x_1 + x_2 = 1 - x_1x_2$得到关于$k$的方程，解方程求出$k$的值，再结合
(1)中$k$的取值范围判断是否存在。
【答案】：
(1)解：
∵方程$x^2 - 2(k - 1)x + k^2 = 0$有两个实数根，
∴$\Delta = [-2(k - 1)]^2 - 4×1×k^2 \geq 0$
$4(k^2 - 2k + 1) - 4k^2 \geq 0$
$4k^2 - 8k + 4 - 4k^2 \geq 0$
$-8k + 4 \geq 0$
$-8k \geq -4$
$k \leq \frac{1}{2}$
(2)解：存在。
由韦达定理得：$x_1 + x_2 = 2(k - 1)$，$x_1x_2 = k^2$
∵$x_1 + x_2 = 1 - x_1x_2$
∴$2(k - 1) = 1 - k^2$
$2k - 2 = 1 - k^2$
$k^2 + 2k - 3 = 0$
$(k + 3)(k - 1) = 0$
$k_1 = -3$，$k_2 = 1$
∵$k \leq \frac{1}{2}$
∴$k = -3$
即存在实数$k = -3$，使得$x_1 + x_2 = 1 - x_1x_2$成立。

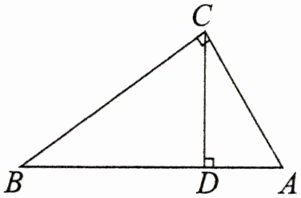
10. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD是斜边AB$上的高。
(1)求证：$AC^{2} = AD \cdot AB$；
(2)若$AC = 6$,$BD = 9$,求$CD$的长。

答案： 【解析】：
(1) 要证明$AC^{2} = AD \cdot AB$，可通过证明三角形相似得到对应边成比例。在$Rt\triangle ABC$中，$CD$是斜边$AB$上的高，所以$\angle ADC = \angle ACB = 90^{\circ}$，又因为$\angle A$是公共角，根据“两角对应相等的两个三角形相似”可证$\triangle ACD \sim \triangle ABC$，从而得出比例式变形即可。
(2) 设$AD = x$，则$AB = AD + BD = x + 9$。由
(1)的结论$AC^{2}=AD\cdot AB$，已知$AC = 6$，可列出方程$6^{2}=x(x + 9)$，解方程求出$AD$的值，再在$Rt\triangle ACD$中，利用勾股定理$CD=\sqrt{AC^{2}-AD^{2}}$求出$CD$的长。
【答案】：
(1)证明：
∵在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$CD$是斜边$AB$上的高
∴$\angle ADC = 90^{\circ}$
∴$\angle ADC=\angle ACB$
∵$\angle A=\angle A$
∴$\triangle ACD\sim\triangle ABC$（两角对应相等的两个三角形相似）
∴$\frac{AC}{AB}=\frac{AD}{AC}$
∴$AC^{2}=AD\cdot AB$
(2)设$AD = x$，则$AB=AD + BD=x + 9$
由
(1)知$AC^{2}=AD\cdot AB$，$AC = 6$
∴$6^{2}=x(x + 9)$
即$36=x^{2}+9x$
$x^{2}+9x - 36=0$
解得$x_{1}=3$，$x_{2}=-12$（舍去）
∴$AD = 3$
在$Rt\triangle ACD$中，$\angle ADC = 90^{\circ}$
$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{6^{2}-3^{2}}=\sqrt{36 - 9}=\sqrt{27}=3\sqrt{3}$
∴$CD$的长为$3\sqrt{3}$