2025年美迪初中衔接暑假河北教育出版社数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年美迪初中衔接暑假河北教育出版社数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
[例2] 解方程:
(1) $ |x - 2| = 3 $;
(2) $ |x + 1| = |x - 3| $。
(1) $ |x - 2| = 3 $;
(2) $ |x + 1| = |x - 3| $。
答案:
【解析】:本题考查解绝对值方程。对于绝对值方程|A|=B(B≥0),其等价于A=B或A=-B。
(1)方程|x - 2| = 3,根据绝对值的性质,可转化为x - 2 = 3或x - 2 = -3,分别求解即可。
(2)方程|x + 1| = |x - 3|,两边平方可消去绝对值符号,得到(x + 1)² = (x - 3)²,展开后求解方程。
【答案】:
(1)解:|x - 2| = 3
∴x - 2 = 3或x - 2 = -3
解得$x_1 = 5$,$x_2 = -1$
(2)解:|x + 1| = |x - 3|
两边平方得:(x + 1)² = (x - 3)²
展开得:$x^2 + 2x + 1 = x^2 - 6x + 9$
移项合并同类项得:8x = 8
解得x = 1
即$x_1 = x_2 = 1$
(1)方程|x - 2| = 3,根据绝对值的性质,可转化为x - 2 = 3或x - 2 = -3,分别求解即可。
(2)方程|x + 1| = |x - 3|,两边平方可消去绝对值符号,得到(x + 1)² = (x - 3)²,展开后求解方程。
【答案】:
(1)解:|x - 2| = 3
∴x - 2 = 3或x - 2 = -3
解得$x_1 = 5$,$x_2 = -1$
(2)解:|x + 1| = |x - 3|
两边平方得:(x + 1)² = (x - 3)²
展开得:$x^2 + 2x + 1 = x^2 - 6x + 9$
移项合并同类项得:8x = 8
解得x = 1
即$x_1 = x_2 = 1$
(1) 根据绝对值的意义脱去绝对值符号求解;(2) 利用两边平方法脱去绝对值符号求解。
解:(1) 由$ |x - 2| = 3 $,得$ x - 2 = 3 或 x - 2 = -3 $,解得$ x = 5 或 x = -1 $。
(2) 由$ |x + 1| = |x - 3| $,两边平方,得$ (x + 1)^2 = (x - 3)^2 $,即$ x^2 + 2x + 1 = x^2 - 6x + 9 $,化简,得$ 8x = 8 $,解得$ x = 1 $。
[反思归纳] (1) $ |ax + b| = c(c > 0) \Leftrightarrow ax + b = c 或 ax + b = -c $(利用绝对值的意义脱去绝对值符号);(2) $ |ax + b| = |cx + d| \Leftrightarrow (ax + b)^2 = (cx + d)^2 $(利用两边平方法脱去绝对值符号)。
解:(1) 由$ |x - 2| = 3 $,得$ x - 2 = 3 或 x - 2 = -3 $,解得$ x = 5 或 x = -1 $。
(2) 由$ |x + 1| = |x - 3| $,两边平方,得$ (x + 1)^2 = (x - 3)^2 $,即$ x^2 + 2x + 1 = x^2 - 6x + 9 $,化简,得$ 8x = 8 $,解得$ x = 1 $。
[反思归纳] (1) $ |ax + b| = c(c > 0) \Leftrightarrow ax + b = c 或 ax + b = -c $(利用绝对值的意义脱去绝对值符号);(2) $ |ax + b| = |cx + d| \Leftrightarrow (ax + b)^2 = (cx + d)^2 $(利用两边平方法脱去绝对值符号)。
答案:
【解析】:本题考查绝对值方程的求解方法。对于形如$|ax + b| = c(c > 0)$的方程,根据绝对值的意义,绝对值符号内的代数式的值为$c$或$-c$,从而将绝对值方程转化为两个一元一次方程求解;对于形如$|ax + b| = |cx + d|$的方程,利用两边平方的方法,可消除绝对值符号,再通过化简求解。
(1) 对于方程$|x - 2| = 3$,依据绝对值的意义,绝对值等于$3$的数有两个,即$3$和$-3$,所以$x - 2 = 3$或$x - 2 = -3$,分别解这两个一元一次方程即可得到$x$的值。
(2) 对于方程$|x + 1| = |x - 3|$,由于等式两边都是绝对值的形式,两边平方后,绝对值符号可去掉,得到$(x + 1)^2 = (x - 3)^2$,然后展开并化简方程,即可求出$x$的值。
【答案】:
(1) 解:由$|x - 2| = 3$,
得$x - 2 = 3$或$x - 2 = -3$,
解得$x = 5$或$x = -1$。
(2) 解:由$|x + 1| = |x - 3|$,
两边平方,得$(x + 1)^2 = (x - 3)^2$,
即$x^2 + 2x + 1 = x^2 - 6x + 9$,
化简,得$8x = 8$,
解得$x = 1$。
(1) 对于方程$|x - 2| = 3$,依据绝对值的意义,绝对值等于$3$的数有两个,即$3$和$-3$,所以$x - 2 = 3$或$x - 2 = -3$,分别解这两个一元一次方程即可得到$x$的值。
(2) 对于方程$|x + 1| = |x - 3|$,由于等式两边都是绝对值的形式,两边平方后,绝对值符号可去掉,得到$(x + 1)^2 = (x - 3)^2$,然后展开并化简方程,即可求出$x$的值。
【答案】:
(1) 解:由$|x - 2| = 3$,
得$x - 2 = 3$或$x - 2 = -3$,
解得$x = 5$或$x = -1$。
(2) 解:由$|x + 1| = |x - 3|$,
两边平方,得$(x + 1)^2 = (x - 3)^2$,
即$x^2 + 2x + 1 = x^2 - 6x + 9$,
化简,得$8x = 8$,
解得$x = 1$。
[例3] 解不等式:
(1) $ |x| < 2 $;
(2) $ |x| \geq 3 $;
(3) $ |x - 1| < 3 $。
(1) $ |x| < 2 $;
(2) $ |x| \geq 3 $;
(3) $ |x - 1| < 3 $。
答案:
【解析】:本题考查绝对值不等式的解法,属于九年级数学内容,题型为解答题中的解不等式题。对于绝对值不等式,需根据绝对值的几何意义或性质进行求解。|x|<a(a>0)的解集为-a<x<a;|x|≥a(a>0)的解集为x≤-a或x≥a;对于|x - b|<c(c>0),可转化为 -c<x - b<c 求解。
【答案】:解:
(1) $ |x| < 2 $
根据绝对值的性质,得$ -2 < x < 2 $
(2) $ |x| \geq 3 $
根据绝对值的性质,得$ x \leq -3 $或$ x \geq 3 $
(3) $ |x - 1| < 3 $
根据绝对值的性质,得$ -3 < x - 1 < 3 $
不等式两边同时加1,得$ -2 < x < 4 $
【答案】:解:
(1) $ |x| < 2 $
根据绝对值的性质,得$ -2 < x < 2 $
(2) $ |x| \geq 3 $
根据绝对值的性质,得$ x \leq -3 $或$ x \geq 3 $
(3) $ |x - 1| < 3 $
根据绝对值的性质,得$ -3 < x - 1 < 3 $
不等式两边同时加1,得$ -2 < x < 4 $
(1)(2) 利用绝对值的几何意义求解;(3) 将$ x - 1 $看作一个整体,利用绝对值的几何意义求解。
解:(1) $ |x| < 2 $,就是数轴上表示$ x $的点到原点的距离小于2,如图所示,
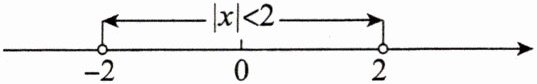
所以原不等式的解为$ -2 < x < 2 $。
(2) $ |x| \geq 3 $,就是数轴上表示$ x $的点到原点的距离大于或等于3,如图所示,
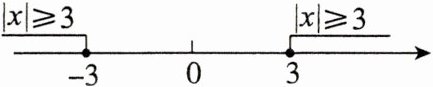
所以原不等式的解为$ x \leq -3 或 x \geq 3 $。
(3) $ |x - 1| < 3 同解于 -3 < x - 1 < 3 $,即$ -2 < x < 4 $,所以原不等式的解为$ -2 < x < 4 $。
[反思归纳] (1) $ |x| < a(a > 0) 的解为 -a < x < a $;(2) $ |x| > a(a > 0) 的解为 x < -a 或 x > a $;(3) $ |ax + b| < c(c > 0) \Leftrightarrow -c < ax + b < c $;(4) $ |ax + b| > c(c > 0) \Leftrightarrow ax + b < -c 或 ax + b > c $。
解:(1) $ |x| < 2 $,就是数轴上表示$ x $的点到原点的距离小于2,如图所示,
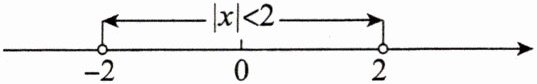
所以原不等式的解为$ -2 < x < 2 $。
(2) $ |x| \geq 3 $,就是数轴上表示$ x $的点到原点的距离大于或等于3,如图所示,
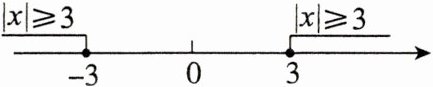
所以原不等式的解为$ x \leq -3 或 x \geq 3 $。
(3) $ |x - 1| < 3 同解于 -3 < x - 1 < 3 $,即$ -2 < x < 4 $,所以原不等式的解为$ -2 < x < 4 $。
[反思归纳] (1) $ |x| < a(a > 0) 的解为 -a < x < a $;(2) $ |x| > a(a > 0) 的解为 x < -a 或 x > a $;(3) $ |ax + b| < c(c > 0) \Leftrightarrow -c < ax + b < c $;(4) $ |ax + b| > c(c > 0) \Leftrightarrow ax + b < -c 或 ax + b > c $。
答案:
【解析】:本题考查绝对值的几何意义及简单绝对值不等式的解法。绝对值的几何意义是数轴上表示数的点到原点的距离,对于形如$|x| < a$($a>0$)的不等式,其解为$-a < x < a$;形如$|x| \geq a$($a>0$)的不等式,其解为$x \leq -a$或$x \geq a$。对于含绝对值的代数式,可将代数式看作一个整体,利用上述结论求解。
(1) 对于$|x| < 2$,根据绝对值的几何意义,数轴上表示$x$的点到原点的距离小于2,所以$x$在$-2$和$2$之间。
(2) 对于$|x| \geq 3$,数轴上表示$x$的点到原点的距离大于或等于3,所以$x$在$-3$及左边或$3$及右边。
(3) 对于$|x - 1| < 3$,将$x - 1$看作一个整体,根据$|A| < a$($a>0$)的解为$-a < A < a$,可得$-3 < x - 1 < 3$,解这个不等式即可得到$x$的范围。
【答案】:
(1) 解:$|x| < 2$,就是数轴上表示$x$的点到原点的距离小于2,
图略
所以原不等式的解为$-2 < x < 2$。
(2) 解:$|x| \geq 3$,就是数轴上表示$x$的点到原点的距离大于或等于3,
图略
所以原不等式的解为$x \leq -3$或$x \geq 3$。
(3) 解:$|x - 1| < 3$同解于$-3 < x - 1 < 3$,
即$-2 < x < 4$,
所以原不等式的解为$-2 < x < 4$。
(1) 对于$|x| < 2$,根据绝对值的几何意义,数轴上表示$x$的点到原点的距离小于2,所以$x$在$-2$和$2$之间。
(2) 对于$|x| \geq 3$,数轴上表示$x$的点到原点的距离大于或等于3,所以$x$在$-3$及左边或$3$及右边。
(3) 对于$|x - 1| < 3$,将$x - 1$看作一个整体,根据$|A| < a$($a>0$)的解为$-a < A < a$,可得$-3 < x - 1 < 3$,解这个不等式即可得到$x$的范围。
【答案】:
(1) 解:$|x| < 2$,就是数轴上表示$x$的点到原点的距离小于2,
图略
所以原不等式的解为$-2 < x < 2$。
(2) 解:$|x| \geq 3$,就是数轴上表示$x$的点到原点的距离大于或等于3,
图略
所以原不等式的解为$x \leq -3$或$x \geq 3$。
(3) 解:$|x - 1| < 3$同解于$-3 < x - 1 < 3$,
即$-2 < x < 4$,
所以原不等式的解为$-2 < x < 4$。
[例4] 解不等式:
(1) $ |x + 3| > |x - 5| $;
(2) $ |x + 2| + |x - 1| < 5 $。
(1) $ |x + 3| > |x - 5| $;
(2) $ |x + 2| + |x - 1| < 5 $。
答案:
【解析】:本题考查绝对值不等式的解法,属于九年级数学内容。对于含绝对值的不等式,可根据绝对值的几何意义或通过分类讨论去掉绝对值符号来求解。
(1) 对于不等式$|x + 3| > |x - 5|$,两边平方可去掉绝对值符号(因为两边均为非负数),得到$(x + 3)^2>(x - 5)^2$,展开后化简求解。
(2) 对于不等式$|x + 2| + |x - 1| < 5$,先找到绝对值内式子为零的点$x=-2$和$x=1$,将数轴分为三段:$x<-2$,$-2≤x≤1$,$x>1$,在每一段内去掉绝对值符号,转化为普通不等式求解,最后取各段解集的并集。
【答案】:
(1) 解:$|x + 3| > |x - 5|$
两边平方得:$(x + 3)^2>(x - 5)^2$
展开得:$x^2 + 6x + 9>x^2 - 10x + 25$
移项合并同类项得:$16x>16$
解得:$x>1$
(2) 解:令$x + 2 = 0$,得$x=-2$;令$x - 1 = 0$,得$x=1$。
当$x<-2$时,原不等式化为$-(x + 2) - (x - 1)<5$
即$-x - 2 - x + 1<5$
$-2x - 1<5$
$-2x<6$
解得$x>-3$,此时解集为$-3<x<-2$。
当$-2≤x≤1$时,原不等式化为$(x + 2) - (x - 1)<5$
即$x + 2 - x + 1<5$
$3<5$,恒成立,此时解集为$-2≤x≤1$。
当$x>1$时,原不等式化为$(x + 2) + (x - 1)<5$
即$2x + 1<5$
$2x<4$
解得$x<2$,此时解集为$1<x<2$。
综上,原不等式的解集为$-3<x<2$。
(1) 对于不等式$|x + 3| > |x - 5|$,两边平方可去掉绝对值符号(因为两边均为非负数),得到$(x + 3)^2>(x - 5)^2$,展开后化简求解。
(2) 对于不等式$|x + 2| + |x - 1| < 5$,先找到绝对值内式子为零的点$x=-2$和$x=1$,将数轴分为三段:$x<-2$,$-2≤x≤1$,$x>1$,在每一段内去掉绝对值符号,转化为普通不等式求解,最后取各段解集的并集。
【答案】:
(1) 解:$|x + 3| > |x - 5|$
两边平方得:$(x + 3)^2>(x - 5)^2$
展开得:$x^2 + 6x + 9>x^2 - 10x + 25$
移项合并同类项得:$16x>16$
解得:$x>1$
(2) 解:令$x + 2 = 0$,得$x=-2$;令$x - 1 = 0$,得$x=1$。
当$x<-2$时,原不等式化为$-(x + 2) - (x - 1)<5$
即$-x - 2 - x + 1<5$
$-2x - 1<5$
$-2x<6$
解得$x>-3$,此时解集为$-3<x<-2$。
当$-2≤x≤1$时,原不等式化为$(x + 2) - (x - 1)<5$
即$x + 2 - x + 1<5$
$3<5$,恒成立,此时解集为$-2≤x≤1$。
当$x>1$时,原不等式化为$(x + 2) + (x - 1)<5$
即$2x + 1<5$
$2x<4$
解得$x<2$,此时解集为$1<x<2$。
综上,原不等式的解集为$-3<x<2$。
(1) 利用两边平方法或绝对值的几何意义求解;(2) 利用零点分段法或绝对值的几何意义求解。
解:(1) 方法一:因为$ |x + 3| \geq 0,|x - 5| \geq 0 $,所以$ |x + 3| > |x - 5| 同解于 (x + 3)^2 > (x - 5)^2 $,即$ x^2 + 6x + 9 > x^2 - 10x + 25 $,化简,得$ 16x > 16 $,解得$ x > 1 $,所以原不等式的解为$ x > 1 $。
方法二:由$ |x + 3| = |x - 5| $,得$ x = 1 $。$ |x + 3| > |x - 5| 的几何意义是数轴上表示 x 的点到 -3 $的距离大于到5的距离。因为数轴上1到$ -3 $的距离等于到5的距离,所以数轴上表示$ x $的点在1的右侧,所以原不等式的解为$ x > 1 $。
(2) 方法一:当$ x < -2 $时,原不等式同解于$ \begin{cases} x < -2, \\ -(x + 2) - (x - 1) < 5, \end{cases} 解得 -3 < x < -2 $;当$ -2 \leq x \leq 1 $时,原不等式同解于$ \begin{cases} -2 \leq x \leq 1, \\ (x + 2) - (x - 1) < 5, \end{cases} 解得 -2 \leq x \leq 1 $;当$ x > 1 $时,原不等式同解于$ \begin{cases} x > 1, \\ (x + 2) + (x - 1) < 5, \end{cases} 解得 1 < x < 2 $。综上,原不等式的解为$ -3 < x < 2 $。
方法二:$ |x + 2| + |x - 1| < 5 的几何意义是数轴上表示 x $的点到1和$ -2 $的两点的距离之和小于5。由数轴可知,$ 1 - (-2) = 3 < 5 $,易知当$ x = -3 或 x = 2 $时,$ |x + 2| + |x - 1| = 5 $,所以$ x 位于 -3 $和2之间(不含端点),所以$ -3 < x < 2 $,所以原不等式的解为$ -3 < x < 2 $。
[反思归纳] (1) $ |x + a| < |x + b| $型的不等式,可用两边平方法脱去绝对值符号,转化为一元一次不等式求解,也可用绝对值的几何意义求解;(2) $ |x + a| \pm |x + b| < c(c > 0) $型的不等式可用零点分段法求解,也可用绝对值的几何意义求解。
解:(1) 方法一:因为$ |x + 3| \geq 0,|x - 5| \geq 0 $,所以$ |x + 3| > |x - 5| 同解于 (x + 3)^2 > (x - 5)^2 $,即$ x^2 + 6x + 9 > x^2 - 10x + 25 $,化简,得$ 16x > 16 $,解得$ x > 1 $,所以原不等式的解为$ x > 1 $。
方法二:由$ |x + 3| = |x - 5| $,得$ x = 1 $。$ |x + 3| > |x - 5| 的几何意义是数轴上表示 x 的点到 -3 $的距离大于到5的距离。因为数轴上1到$ -3 $的距离等于到5的距离,所以数轴上表示$ x $的点在1的右侧,所以原不等式的解为$ x > 1 $。
(2) 方法一:当$ x < -2 $时,原不等式同解于$ \begin{cases} x < -2, \\ -(x + 2) - (x - 1) < 5, \end{cases} 解得 -3 < x < -2 $;当$ -2 \leq x \leq 1 $时,原不等式同解于$ \begin{cases} -2 \leq x \leq 1, \\ (x + 2) - (x - 1) < 5, \end{cases} 解得 -2 \leq x \leq 1 $;当$ x > 1 $时,原不等式同解于$ \begin{cases} x > 1, \\ (x + 2) + (x - 1) < 5, \end{cases} 解得 1 < x < 2 $。综上,原不等式的解为$ -3 < x < 2 $。
方法二:$ |x + 2| + |x - 1| < 5 的几何意义是数轴上表示 x $的点到1和$ -2 $的两点的距离之和小于5。由数轴可知,$ 1 - (-2) = 3 < 5 $,易知当$ x = -3 或 x = 2 $时,$ |x + 2| + |x - 1| = 5 $,所以$ x 位于 -3 $和2之间(不含端点),所以$ -3 < x < 2 $,所以原不等式的解为$ -3 < x < 2 $。
[反思归纳] (1) $ |x + a| < |x + b| $型的不等式,可用两边平方法脱去绝对值符号,转化为一元一次不等式求解,也可用绝对值的几何意义求解;(2) $ |x + a| \pm |x + b| < c(c > 0) $型的不等式可用零点分段法求解,也可用绝对值的几何意义求解。
答案:
【解析】:本题考查绝对值不等式的求解。(1)对于$|x + 3|>|x - 5|$,可利用两边平方法,因为绝对值非负,平方后不等号方向不变,转化为一元一次不等式求解;也可根据绝对值几何意义,即数轴上点到$-3$和$5$的距离大小关系求解。(2)对于$|x + 2| + |x - 1|<5$,零点分段法是根据绝对值内式子为零的点分区间讨论,去掉绝对值符号求解;几何意义是数轴上点到$-2$和$1$的距离之和小于$5$,结合数轴找到满足条件的区间。
【答案】:(1)原不等式的解为$x>1$;(2)原不等式的解为$-3<x<2$
【答案】:(1)原不等式的解为$x>1$;(2)原不等式的解为$-3<x<2$
查看更多完整答案,请扫码查看


