《2025年假期新思维八年级数学北师大版》

19.(7分)如图,在△ABC中,∠ACB= 90°,BE平分∠ABC,DE⊥AB于D,如果AC= 3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系？请说明理由.

答案： 解：AE + DE = AC = 3 cm. 理由如下：
∵ ∠ACB = 90°，BE 平分 ∠ABC，DE⊥AB，
∴ DE = CE，
由图可知，AC = AE + CE，
∴ AC = AE + DE = 3 cm.

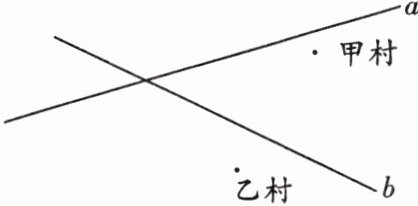
20.(8分)已知甲村和乙村靠近公路a、b,为了发展经济,甲乙两村准备合建一个工厂,经协商,工厂必须满足以下要求：
(1)到两村的距离相等；
(2)到两条公路的距离相等.你能帮忙确定工厂的位置吗？

答案：
解：①以 O 为圆心，以任意长为半径画弧，分别交直线 a、b 于点 A、B；
②分别以 A、B 为圆心，以大于 $\frac{1}{2}$AB 为半径画弧，两弧相交于点 C，连接 OC；
③连接 ED，分别以 E、D 为圆心，以大于 $\frac{1}{2}$ED 为半径画弧，两弧相交于 F、G 两点，连接 FG；
④FG 与 OC 相交于点 H，则 H 即为工厂的位置.

21.(9分)如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE= BD,求证：
(1)△ABD≌△ACE；
(2)△ADE为等边三角形.

答案： 【证明】
(1)
∵ △ABC 是等边三角形，
∴ AB = AC，∠BAC = ∠B = ∠ACB = 60°，
∴ ∠ACD = 120°，
∵ CE 平分 ∠ACD，
∴ ∠ACE = $\frac{1}{2}$∠ACD = 60°，
∴ ∠ACE = ∠B，
在 △ABD 和 △ACE 中 $\begin{cases}AB = AC\\∠B = ∠ACE\\BD = CE\end{cases}$，
∴ △ABD ≌ △ACE(SAS)；
(2)
∵ △ABD ≌ △ACE，
∴ AD = AE，∠CAE = ∠BAD，
∴ ∠DAE = ∠BAC = 60°，
∴ △ADE 为等边三角形.

22.(9分)如图1,已知∠ABC= 90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.

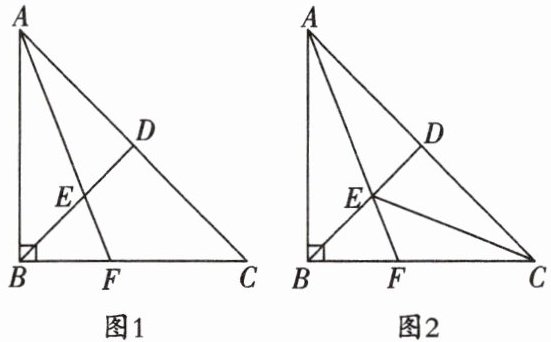
(1)求证：BE= BF；
(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.

答案：
(1)【证明】
∵ ∠ABC = 90°，BA = BC，点 D 为斜边 AC 的中点，
∴ BD⊥AC，∠DBC = 45°，
∵ AF 是 ∠BAC 的平分线，
∴ ∠BAF = 22.5°，
∴ ∠BFE = 67.5°，
∴ ∠BEF = 180° - ∠EBF - ∠EFB = 67.5°，
∴ ∠BFE = ∠BEF，
∴ BE = BF；
(2)
∵ ∠ABC = 90°，BA = BC，点 D 为斜边 AC 的中点，
∴ BD = AD = CD，
∴ △ABD、△CBD 是等腰三角形，
由已知得，△ABC 是等腰三角形，
由
(1)得，△BEF 是等腰三角形，
∵ AF 是 ∠BAC 的平分线，BD 是 ∠ABC 的平分线，
∵ △ABC 为等腰三角形，D 为 AC 中点，
∴ BD 垂直平分 AC，
∴ EA = EC，
∴ △AEC 是等腰三角形.

23.(12分)(1)如图1,点P是等腰三角形ABC的底边BC上的一个动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R,请观察AR与AQ,它们有何数量关系？并证明你的猜想.
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗？请你在图2中完成图形,并直接写出结论.

答案：
解：
(1) AR = AQ，证明如下：
∵ △ABC 是等腰三角形，
∴ AB = AC，∠B = ∠C，
又
∵ PR⊥BC，
∴ ∠RPC = 90°，
∴ ∠C + ∠R = 90°，
∠B + ∠BQP = 90°，
∵ ∠BQP = ∠AQR，
∴ ∠AQR = ∠R，
∴ AR = AQ；
(2) AR = AQ 仍然成立：
∵ △ABC 是等腰三角形，
∴ AB = AC，∠ABC = ∠C，又
∵ PR⊥BC，
∴ ∠RPC = 90°，
∴ ∠C + ∠R = 90°，∠PBQ + ∠BQP = 90°，
∵ ∠ABC = ∠PBQ，
∴ ∠AQR = ∠R，
∴ AR = AQ.