《2025年假期新思维八年级数学北师大版》

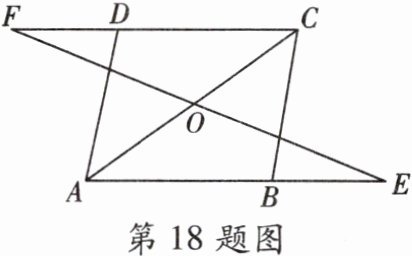
18. (7分)已知：如图,在□ABCD中,延长AB至点E,延长CD至点F,使得BE= DF。连接EF,与对角线AC交于点O。求证：OE= OF。

答案： 【证明】
∵四边形ABCD是平行四边形，
∴ $ AB // CD $，$ AB = CD $，
∵ $ BE = DF $，
∴ $ AB + BE = CD + DF $，即 $ AE = CF $，
∵ $ AB // CD $，
∴ $ AE // CF $，
∴ $ \angle E = \angle F $，$ \angle OAE = \angle OCF $，在 $ \triangle AOE $ 和 $ \triangle COF $ 中，$ \left\{ \begin{array} { l } { \angle E = \angle F } \\ { AE = CF } \\ { \angle OAE = \angle OCF } \end{array} \right. $，
∴ $ \triangle AOE \cong \triangle COF (ASA) $，
∴ $ OE = OF $.

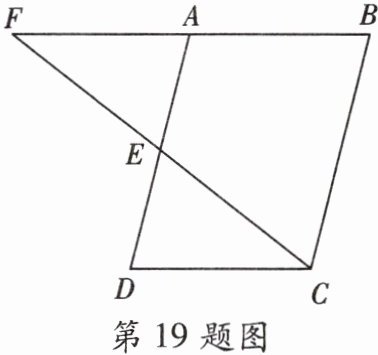
19. (7分)如图,E是□ABCD的边AD的中点,连接CE并延长,交BA的延长线于F,若CD= 6,求BF的长。

答案： 解：
∵E是□ABCD的边AD的中点，
∴AE=DE，
∵四边形ABCD是平行四边形，
∴AB=CD=6，AB//CD，
∴∠F=∠DCE，
在△AEF和△DEC中，
$\left\{ \begin{array}{l} \angle F = \angle DCE \\ \angle AEF = \angle DEC \\ AE = DE \end{array} \right.$，
∴△AEF≌△DEC(AAS)，
∴AF=CD=6，
∴BF=AB+AF=6+6=12。

20. (8分)在一个多边形中,一个内角相邻的外角与其他各内角的和为600°。
(1)如果这个多边形是五边形,请求出这个外角的度数；
(2)是否存在符合题意的其他多边形？如果存在,请求出边数及这个外角的度数；如果不存在,请说明理由。

答案： 解：（1）设这个外角的度数是 $ x^{\circ} $，则 $ ( 5 - 2 ) × 180 - ( 180 - x ) + x = 600 $，解得 $ x = 120 $. 故这个外角的度数是 $ 120^{\circ} $.
（2）存在. 设边数为n，这个外角的度数是 $ x^{\circ} $，则 $ ( n - 2 ) × 180 - ( 180 - x ) + x = 600 $，整理得 $ x = 570 - 90n $，
∵ $ 0 ＜ x ＜ 180 $，即 $ 0 ＜ 570 - 90n ＜ 180 $，并且n为正整数，
∴ $ n = 5 $ 或 $ n = 6 $.
故这个多边形的边数是6，这个外角的度数为 $ 30^{\circ} $.

21. (9分)我们给出如下定义：若一个四边形有一组对边相等,另一组对边不相等,则称这个四边形为等对边四边形。
(1)写出你所学过的特殊四边形中是等对边四边形的一种图形的名称；
(2)请你探究：等对边四边形另一组对边中点的连线段与等对边中一条线段长度的大小关系,并证明你的结论。(写出已知、求证与证明)

答案：
解：（1）等腰梯形；
（2）另一组对边中点的连线段小于等对边中一条线段长度；
已知：四边形ABCD，$ AB = CD $，点E，F分别是AD，BC的中点，求证：$ EF ＜ AB $.
【证明】连接AC，取AC的中点G，连接EG，FG，
∵点E，F分别是AD，BC的中点，
∴ $ AE = DE $，$ BF = CF $，
∴ $ EG = \frac{1}{2}CD $，$ GF = \frac{1}{2}AB $，
∵ $ AB = CD $，
∴ $ GE + GF = AB = CD $，在 $ \triangle EFG $ 中，$ EG + FG ＞ EF $，
∴ $ EF ＜ AB $.