《2025年假期新思维八年级数学北师大版》

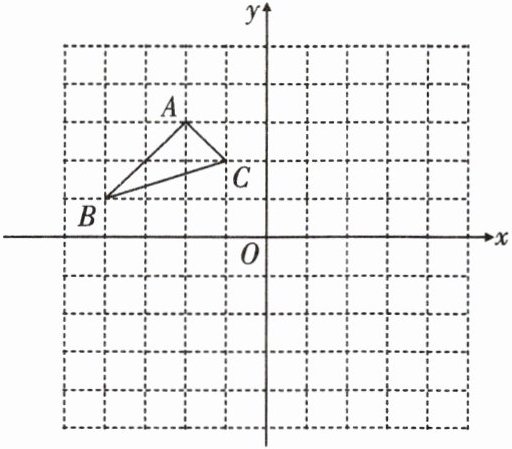
20. (8分)如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的$△A_1B_1C_1($只画出图形).
(2)作出△ABC关于原点O成中心对称的$△A_2B_2C_2($只画出图形),写出$B_2$和$C_2$的坐标.

答案：
解:
(1)$ \triangle A_{1}B_{1}C_{1} $ 如图所示;
(2)$ \triangle A_{2}B_{2}C_{2} $ 如图所示,$ B_{2}(4,-1),C_{2}(1,-2) $.

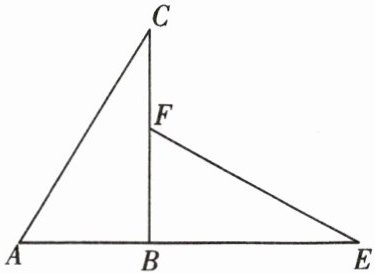
21. (9分)如图,△ABC是直角三角形,延长AB到点E,使BE= BC,在BC上取一点F,使BF= AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AC与EF的关系如何?

答案： 解:
(1)
∵ $ BC = BE,BA = BF $,
∴ $ BC $ 和 $ BE,BA $ 和 $ BF $ 为对应边,
∵ $ \triangle ABC $ 旋转后能与 $ \triangle FBE $ 重合,
∴ 旋转中心为点 $ B $;
(2)
∵ $ \angle ABC = 90^{\circ} $,而 $ \triangle ABC $ 旋转后能与 $ \triangle FBE $ 重合,
∴ $ \angle ABF $ 等于旋转角,
∴ 旋转了 $ 90 $ 度;
(3)$ AC = EF,AC \perp EF $. 理由如下:
∵ $ \triangle ABC $ 绕点 $ B $ 顺时针旋转 $ 90^{\circ} $ 后能与 $ \triangle FBE $ 重合,
∴ $ EF = AC,EF $ 与 $ AC $ 成 $ 90^{\circ} $ 的角,即 $ AC \perp EF $.

22. (9分)阅读理解,并解答问题:
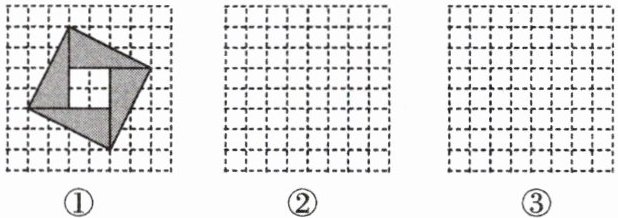
如图所示的8×8网格都是由边长为1的小正方形组成,图①中的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽通过对这种图形切割、拼接,巧妙地利用面积关系证明了著名的勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国数学史上的骄傲.

问题:
请用“赵爽弦图”中的四个直角三角形通过你所学过的图形变化,在图②,图③的方格纸中设计另外两个不同的图案,每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠.画图要求:
(1)图②中所设计的图案(不含方格纸)必须是轴对称图形但不是中心对称图形;
(2)图③中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.

答案：
解:
(1)图②是轴对称图形而不是中心对称图形;
(2)如图③既是轴对称图形,又是中心对称图形.

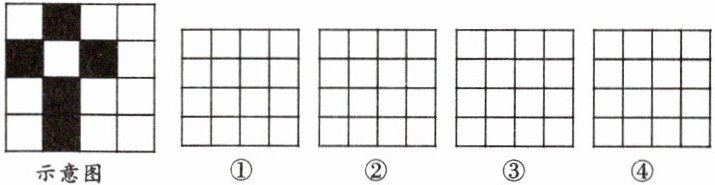
23. (广安中考)(12分)在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
要求:(1)5个小正方形必须相连(有公共边或公共顶点视为相连)
(2)将选中的小正方形方格用黑色签字笔涂成阴影图形.(若两个方案的图形经过翻折、平移、旋转后能够重合,均视为一种方案)

答案：
解:如图.