2025年假期新思维八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期新思维八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
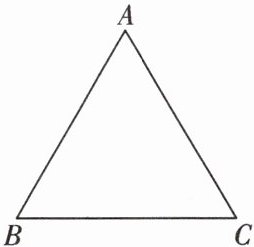
15. (6分)将正三角形ABC绕它的顶点C按顺时针方向旋转90°,作出旋转后的图形.

答案:
解:如图所示,$ \triangle A'B'C $ 就是所要求作的三角形.
解:如图所示,$ \triangle A'B'C $ 就是所要求作的三角形.

16. (6分)已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,求a与b的值.
答案:
解:
∵ 点 $ A(2a + 2,3 - 3b) $ 与点 $ B(2b - 4,3a + 6) $ 关于坐标原点对称,
∴ $ \begin{cases} 2a + 2 + 2b - 4 = 0 \\ 3 - 3b + 3a + 6 = 0 \end{cases} $,解得: $ \begin{cases} a = -1 \\ b = 2 \end{cases} $
∵ 点 $ A(2a + 2,3 - 3b) $ 与点 $ B(2b - 4,3a + 6) $ 关于坐标原点对称,
∴ $ \begin{cases} 2a + 2 + 2b - 4 = 0 \\ 3 - 3b + 3a + 6 = 0 \end{cases} $,解得: $ \begin{cases} a = -1 \\ b = 2 \end{cases} $
17. (6分)如图,在Rt△ABC中,∠ACB= 90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B、C、E在同一直线上.
(1)求旋转角的大小;
(2)若AB= 10,AC= 8,求BE的长.
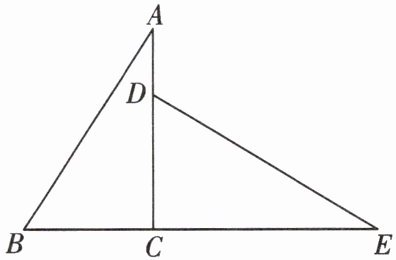
(1)求旋转角的大小;
(2)若AB= 10,AC= 8,求BE的长.

答案:
解:
(1)
∵ $ \triangle EDC $ 是 $ \triangle ABC $ 绕着点 $ C $ 顺时针方向旋转得到的,此时点 $ B $、$ C $、$ E $ 在同一直线上,
∴ $ \angle ACE = 90^{\circ} $,即旋转角为 $ 90^{\circ} $.
(2)在 $ \text{Rt} \triangle ABC $ 中,
∵ $ AB = 10,AC = 8 $,
∴ $ BC = \sqrt{AB^{2} - AC^{2}} = 6 $,
∵ $ \triangle ABC $ 绕着点 $ C $ 旋转得到 $ \triangle DCE $,
∴ $ CE = CA = 8 $,
∴ $ BE = BC + CE = 6 + 8 = 14 $.
(1)
∵ $ \triangle EDC $ 是 $ \triangle ABC $ 绕着点 $ C $ 顺时针方向旋转得到的,此时点 $ B $、$ C $、$ E $ 在同一直线上,
∴ $ \angle ACE = 90^{\circ} $,即旋转角为 $ 90^{\circ} $.
(2)在 $ \text{Rt} \triangle ABC $ 中,
∵ $ AB = 10,AC = 8 $,
∴ $ BC = \sqrt{AB^{2} - AC^{2}} = 6 $,
∵ $ \triangle ABC $ 绕着点 $ C $ 旋转得到 $ \triangle DCE $,
∴ $ CE = CA = 8 $,
∴ $ BE = BC + CE = 6 + 8 = 14 $.
18. (7分)在平面直角坐标系中,已知点A(1,1),B(3,1),C(3,2),D(1,2),将四边形ABCD向下平移3个单位,得到四边形$A_1B_1C_1D_1.$请根据题意在平面直角坐标系中画出这两个四边形.
答案:
解:如图所示,四边形 $ ABCD $ 以及四边形 $ A_{1}B_{1}C_{1}D_{1} $ 即为所求.
解:如图所示,四边形 $ ABCD $ 以及四边形 $ A_{1}B_{1}C_{1}D_{1} $ 即为所求.

19. (7分)将△ABC沿BC的方向平移得到△DEF.
(1)若∠B= 74°,∠F= 26°,求∠A的度数;
(2)若BC= 4.5cm,EC= 3.5cm,求△ABC平移的距离.
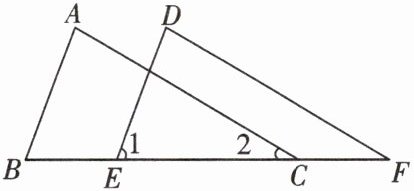
(1)若∠B= 74°,∠F= 26°,求∠A的度数;
(2)若BC= 4.5cm,EC= 3.5cm,求△ABC平移的距离.

答案:
解:
(1)由图形平移的特征可知 $ \triangle ABC $ 和 $ \triangle DEF $ 的形状与大小相同,即 $ \triangle ABC \cong \triangle DEF $,
∴ $ \angle 2 = \angle F = 26^{\circ} $,
∵ $ \angle B = 74^{\circ} $,
∴ $ \angle A = 180^{\circ} - (\angle 2 + \angle B) = 180^{\circ} - (26^{\circ} + 74^{\circ}) = 80^{\circ} $;
(2)
∵ $ BC = 4.5 \text{ cm},EC = 3.5 \text{ cm} $,
∴ $ BE = BC - EC = 4.5 - 3.5 = 1 \text{ cm} $,
∴ $ \triangle ABC $ 平移的距离为 $ 1 \text{ cm} $.
(1)由图形平移的特征可知 $ \triangle ABC $ 和 $ \triangle DEF $ 的形状与大小相同,即 $ \triangle ABC \cong \triangle DEF $,
∴ $ \angle 2 = \angle F = 26^{\circ} $,
∵ $ \angle B = 74^{\circ} $,
∴ $ \angle A = 180^{\circ} - (\angle 2 + \angle B) = 180^{\circ} - (26^{\circ} + 74^{\circ}) = 80^{\circ} $;
(2)
∵ $ BC = 4.5 \text{ cm},EC = 3.5 \text{ cm} $,
∴ $ BE = BC - EC = 4.5 - 3.5 = 1 \text{ cm} $,
∴ $ \triangle ABC $ 平移的距离为 $ 1 \text{ cm} $.
查看更多完整答案,请扫码查看


