搜索
公式
(1)有些同类事物中的数量关系常常可以用公式来描述. 例如,在行程问题中,用 $ s $ 表示路程, $ v $ 表示速度, $ t $ 表示时间,就可以得到路程公式 $ s = $____.
(2)在小学,我们学习过许多公式,如长方形、正方形、三角形、梯形、圆等图形的面积公式,长方体、正方体等图形的体积公式,等等.
(1)有些同类事物中的数量关系常常可以用公式来描述. 例如,在行程问题中,用 $ s $ 表示路程, $ v $ 表示速度, $ t $ 表示时间,就可以得到路程公式 $ s = $____.
(2)在小学,我们学习过许多公式,如长方形、正方形、三角形、梯形、圆等图形的面积公式,长方体、正方体等图形的体积公式,等等.
答案：
vt
1. 如图,若 $ a = 10 $, $ b = 4 $,则这个图形的面积是( )
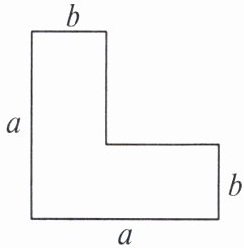
A.32
B.42
C.80
D.64
A.32
B.42
C.80
D.64
答案：
D 解析如图所示
白色部分图形的面积为$a^{2}-(a-b)^{2}$.当$a=10,b=4$时，$a^{2}-(a-b)^{2}=10^{2}-(10-4)^{2}=64$.
D 解析如图所示
白色部分图形的面积为$a^{2}-(a-b)^{2}$.当$a=10,b=4$时，$a^{2}-(a-b)^{2}=10^{2}-(10-4)^{2}=64$. 2. 若 $ a $, $ b $ 分别表示长方形的长和宽,则
(1)长方形的周长 $ l = $____,面积 $ S = $____;
(2)当 $ a = 2 \mathrm{cm} $, $ b = 3 \mathrm{cm} $ 时,周长 $ l = $____ $ \mathrm{cm} $,面积 $ S = $____ $ \mathrm{cm}^2 $.
(1)长方形的周长 $ l = $____,面积 $ S = $____;
(2)当 $ a = 2 \mathrm{cm} $, $ b = 3 \mathrm{cm} $ 时,周长 $ l = $____ $ \mathrm{cm} $,面积 $ S = $____ $ \mathrm{cm}^2 $.
答案：
(1)$2a+2b$ $ab$
(2)10 6
(1)$2a+2b$ $ab$
(2)10 6
3. 如图,阴影部分面积为 $ 40 \mathrm{cm}^2 $,圆环的面积是多少? (结果用含 $ \pi $ 的式子表示)
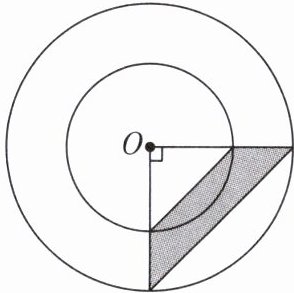
答案：
解 设外圆半径为$R\ cm$，内圆半径为$r\ cm$，$S_{阴影}=\frac{1}{2}(R^{2}-r^{2})=40$，则$R^{2}-r^{2}=80$.圆环的面积为$\pi(R^{2}-r^{2})=80\pi\ cm^{2}$.
4. 已知圆锥的体积 $ V = \frac{1}{3} \pi r^2 h $,其中 $ r $ 为底面半径, $ h $ 为圆锥的高. 当 $ r = 3 \mathrm{cm} $, $ h = 4 \mathrm{cm} $ 时,则圆锥的体积为____.
答案：
$12\pi\ cm^{3}$ 解析 当$r=3\ cm$，$h=4\ cm$时，$V=\frac{1}{3}×\pi×3^{2}×4=12\pi(cm^{3})$.
5. 某木工师傅制作的一个工件如图中阴影部分所示.
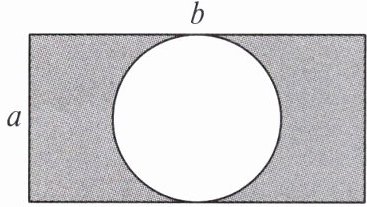
(1)用代数式表示工件的面积.
(2)当 $ a = 8 \mathrm{cm} $, $ b = 12 \mathrm{cm} $ 时,工件的面积是多少? (结果用含 $ \pi $ 的式子表示)
(1)用代数式表示工件的面积.
(2)当 $ a = 8 \mathrm{cm} $, $ b = 12 \mathrm{cm} $ 时,工件的面积是多少? (结果用含 $ \pi $ 的式子表示)
答案：
解
(1)工件的面积$S=ab-\frac{\pi a^{2}}{4}$.
(2)当$a=8\ cm$，$b=12\ cm$时，工件的面积$S=8×12-\frac{\pi×8^{2}}{4}=(96-16\pi)cm^{2}$.
(1)工件的面积$S=ab-\frac{\pi a^{2}}{4}$.
(2)当$a=8\ cm$，$b=12\ cm$时，工件的面积$S=8×12-\frac{\pi×8^{2}}{4}=(96-16\pi)cm^{2}$.
查看更多完整答案，请扫码查看
