7. 根据数字排列规律,自主探究,回答下列问题。
(1)在 $A$ 处的是正数还是负数?
(2)负数排在 $A,B,C,D$ 中的什么位置?
(3)第 $1234$ 个数是正数还是负数?排在对应于 $A,B,C,D$ 中的什么位置?
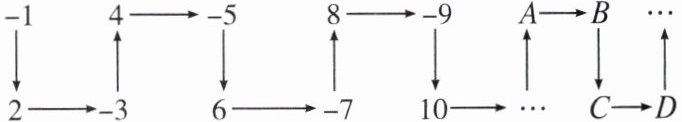
(1)在 $A$ 处的是正数还是负数?
(2)负数排在 $A,B,C,D$ 中的什么位置?
(3)第 $1234$ 个数是正数还是负数?排在对应于 $A,B,C,D$ 中的什么位置?
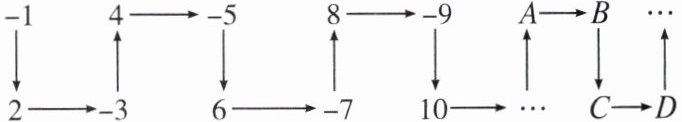
答案:
解
(1)因为在A处的是向上箭头的上方对应的数,与4的符号相同,所以在A处的数是正数.
(2)观察不难发现,向下箭头的上方的数是负数,下方是正数,向上箭头的下方是负数,上方是正数,所以负数排在A,B,C,D中的B和D位置处.
(3)因为1234÷4=308……2,所以第1234个数排在类似C的位置,是正数.
(1)因为在A处的是向上箭头的上方对应的数,与4的符号相同,所以在A处的数是正数.
(2)观察不难发现,向下箭头的上方的数是负数,下方是正数,向上箭头的下方是负数,上方是正数,所以负数排在A,B,C,D中的B和D位置处.
(3)因为1234÷4=308……2,所以第1234个数排在类似C的位置,是正数.
1. 数轴及其画法
(1) 在数学中,可以用一条直线上的点表示数,它满足以下三个条件:
① 在直线上任取一个点表示数 0,这个点叫作____;
② 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为____方向;
③ 选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示 1,2,3,…;从原点向____,用类似方法依次表示 -1,-2,-3,…。
(2) 0 是正数和负数的分界,原点是数轴的“基准点”。
(3) 像这样,规定了____、____和____的____叫作数轴。
原点将数轴(原点除外)分成两部分,其中正方向一侧的部分叫作数轴的____半轴;另一侧的部分叫作数轴的____半轴。
(1) 在数学中,可以用一条直线上的点表示数,它满足以下三个条件:
① 在直线上任取一个点表示数 0,这个点叫作____;
② 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为____方向;
③ 选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示 1,2,3,…;从原点向____,用类似方法依次表示 -1,-2,-3,…。
(2) 0 是正数和负数的分界,原点是数轴的“基准点”。
(3) 像这样,规定了____、____和____的____叫作数轴。
原点将数轴(原点除外)分成两部分,其中正方向一侧的部分叫作数轴的____半轴;另一侧的部分叫作数轴的____半轴。
答案:
(1)①原点 ②负 ③左
(3)原点 正方向 单位长度 直线 正 负
(1)①原点 ②负 ③左
(3)原点 正方向 单位长度 直线 正 负
2. 有理数与数轴上点的对应关系
一般地,设 $ a $ 是一个正数,则数轴上表示数 $ a $ 的点在数轴的____半轴上,与原点的距离是____个单位长度;表示数 $ -a $ 的点在数轴的____半轴上,与原点的距离是____个单位长度。数轴上与原点的距离是 $ a $ 个单位长度的点,简称为数轴上与原点的距离是____的点。
一般地,设 $ a $ 是一个正数,则数轴上表示数 $ a $ 的点在数轴的____半轴上,与原点的距离是____个单位长度;表示数 $ -a $ 的点在数轴的____半轴上,与原点的距离是____个单位长度。数轴上与原点的距离是 $ a $ 个单位长度的点,简称为数轴上与原点的距离是____的点。
答案:
正 a 负 a a
1. 下列说法:
① 规定了原点、正方向的直线是数轴;
② 数轴上两个不同的点不可以表示同一个有理数;
③ 任何一个有理数都可以在数轴上找到与它对应的唯一点。
其中正确的是( )
A.①
B.②③
C.③
D.①②
① 规定了原点、正方向的直线是数轴;
② 数轴上两个不同的点不可以表示同一个有理数;
③ 任何一个有理数都可以在数轴上找到与它对应的唯一点。
其中正确的是( )
A.①
B.②③
C.③
D.①②
答案:
B
2. 在数轴上,点 $ A $ 表示的数是 -2,从点 $ A $ 出发,沿数轴向某一方向移动 5 个单位长度到达点 $ B $,则点 $ B $ 表示的数是( )
A.3
B.±7
C.3 或 -7
D.-3 或 7
A.3
B.±7
C.3 或 -7
D.-3 或 7
答案:
C
查看更多完整答案,请扫码查看


