搜索
8. 观察下列按一定规律排列的单项式：$-a$,$0$,$a^{2}$,$0$,$-a^{3}$,$0$,$a^{4}$,$0$,…$$,则第 2 025 个单项式为( )
A.$-a^{2025}$
B.0
C.$-a^{1013}$
D.$a^{1013}$
A.$-a^{2025}$
B.0
C.$-a^{1013}$
D.$a^{1013}$
答案：
D 解析根据题意，知偶数位置对应的单项式均为0.奇数位置对应的单项式中，第1项，系数为−1,指数为$\frac{1+1}{2}$=1;第3项，系数为1,指数为$\frac{1+3}{2}$=2;第5项，系数为−1，指数为$\frac{1+5}{2}$=3;第7项，系数为1,指数为$\frac{1+7}{2}$=4;则第2025个单项式的系数为1,指数为$\frac{1+2025}{2}$=1013,即为a¹⁰¹³.故选D.
9. 如图,线段$AB= 24\ cm$,动点$P从点A$出发,以$2\ cm/s的速度沿AB$运动,$M为线段AP$的中点,$N为线段BP$的中点. 以下说法正确的是( )
①运动$4\ s$后,$PB= 2AM$；
②$PM + MN$的值随着运动时间的改变而改变；
③$2BM - BP$的值不变.
A.①②
B.③
C.①②③
D.②③
①运动$4\ s$后,$PB= 2AM$；
②$PM + MN$的值随着运动时间的改变而改变；
③$2BM - BP$的值不变.
A.①②
B.③
C.①②③
D.②③
答案：
D 解析运动4s后,AP=2×4=8(cm),PB=AB−AP=16(cm).因为M为线段AP的中点，所以AM=$\frac{1}{2}$AP=4cm,所以4AM=PB,故①错误;设运动ts,则AP=2tcm,PB=24−2t(其中t大于或等于0,且t＜12)cm,因为M为线段AP的中点，N为BP的中点，所以AM=PM=$\frac{1}{2}$AP=tcm,PN=BN=$\frac{1}{2}$PB=12−t(cm).所以PM+MN=PM+PM+PN=12+t(cm).所以PM+MN的值随着运动时间的改变而改变，故②正确;因为BM=AB−AM=24−t(cm),PB=24−2t(t大于或等于0,且t＜12)(cm)，所以2BM−BP=2(24−t)−(24−2t)=24(cm),所以2BM−BP的值不变，故③正确.故选D.
10. 已知$\angle AOB= 20^{\circ}$,$\angle AOC= 4\angle AOB$,$OD平分\angle AOB$,$OM平分\angle AOC$,则$\angle MOD$的度数是( )
A.$20^{\circ}或50^{\circ}$
B.$20^{\circ}或60^{\circ}$
C.$30^{\circ}或50^{\circ}$
D.$30^{\circ}或60^{\circ}$
A.$20^{\circ}或50^{\circ}$
B.$20^{\circ}或60^{\circ}$
C.$30^{\circ}或50^{\circ}$
D.$30^{\circ}或60^{\circ}$
答案：
C 解析分为两种情况:如图1,当∠AOB在∠AOC内部时，
因为∠AOB=20°,∠AOC=4∠AOB,所以∠AOC=80°.因为OD平分∠AOB，OM平分∠AOC，所以∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°,∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°.所以∠MOD=∠AOM−∠AOD=40°−10°=30°.如图2,当∠AOB在∠AOC外部时，
因为∠AOB=20°,∠AOC=4∠AOB,所以∠AOC=80°.因为OD平分∠AOB，OM平分∠AOC，所以∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°,∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°.所以∠MOD=∠AOM+∠AOD=40°+10°=50°.综上所述，∠MOD的度数为30°或50°.
C 解析分为两种情况:如图1,当∠AOB在∠AOC内部时，
因为∠AOB=20°,∠AOC=4∠AOB,所以∠AOC=80°.因为OD平分∠AOB，OM平分∠AOC，所以∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°,∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°.所以∠MOD=∠AOM−∠AOD=40°−10°=30°.如图2,当∠AOB在∠AOC外部时， 因为∠AOB=20°,∠AOC=4∠AOB,所以∠AOC=80°.因为OD平分∠AOB，OM平分∠AOC，所以∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°,∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°.所以∠MOD=∠AOM+∠AOD=40°+10°=50°.综上所述，∠MOD的度数为30°或50°. 11. 计算：$(-2)÷ (-5)× \dfrac{1}{5}= $______.
答案：
$\frac{2}{25}$ 解析原式=2×$\frac{1}{5}$×$\frac{1}{5}$=$\frac{2}{25}$.
12. 当$m$的值为______时,$5x^{3}-2x - 1与4mx + 3的和不含x$的一次项.
答案：
$\frac{1}{2}$ 解析5x³−2x−1+4mx+3=5x³+(4m−2)x+2,由和不含x的一次项，知4m−2=0,解得m=$\frac{1}{2}$.
13. 在手工制作课上,老师组织七年级一班的学生用硬纸制作圆柱形茶叶筒. 七年级一班共有学生 50 人,每名学生每小时剪筒身 40 个或剪筒底 120 个. 要求一个筒身配两个筒底,那么安排______人剪筒身,才能使每小时剪出的筒身与筒底恰好配套.
答案：
30 解析设x人剪筒身，则(50−x)人剪筒底，根据每小时剪出的筒身与筒底恰好配套，列得方程2×40x=120(50−x),解得x=30.安排30人剪筒身，才能使每小时剪出的筒身与筒底恰好配套.
14. 已知$A$,$B$,$C$三点在同一条直线上,若$D$,$E分别为线段AB$,$BC$的中点,且$AB= 80$,$BC= 60$,则线段$DE$的长为______.
答案：
70或10 解析因为D是线段AB的中点，AB=80,所以AD=BD=$\frac{1}{2}$AB=40.因为E是线段BC的中点，BC=60，所以BE=CE=$\frac{1}{2}$BC=30.分两种情况讨论:如图1,当点C在线段AB的延长线上时，DE=BD+BE=70.
如图2,当点C在线段AB上时，DE=BD−BE=10.
故答案为70或10.
70或10 解析因为D是线段AB的中点，AB=80,所以AD=BD=$\frac{1}{2}$AB=40.因为E是线段BC的中点，BC=60，所以BE=CE=$\frac{1}{2}$BC=30.分两种情况讨论:如图1,当点C在线段AB的延长线上时，DE=BD+BE=70.
如图2,当点C在线段AB上时，DE=BD−BE=10. 故答案为70或10. 15. 2025 年元旦,小颖在一张长方形宣纸上的四个正方形格子中写下了“元旦快乐”的毛笔书法作品,如图所示. 已知宣纸的长为$108\ cm$,正方形格子的边长相等,正方形格子与纸边之间的边空宽相等,相邻两个字的字距相等,且边空宽、字宽、字距之比为$3:6:2$,则这张长方形宣纸的面积为______$cm^{2}$.
答案：
3888 解析因为边空宽、字宽、字距之比为3:6:2,所以设边空宽为3xcm，则字宽、字距分别为6xcm,2xcm.因为宣纸的长为108cm，正方形格子的边长相等，正方形格子与纸边之间的边空宽相等，相邻两个字的字距相等，所以3x×2+6x×4+2x×3=108,解得x=3,所以宣纸的宽为3x×2+6x=12x=36(cm).所以这张长方形宣纸的面积为108×36=3888(cm²).
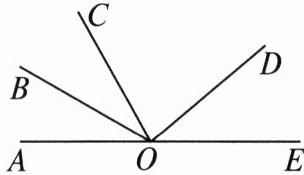
16. 如图,已知$O是直线AE$上一点,$OC$是一条射线,$OB平分\angle AOC$,$OD在\angle COE$内,$\angle COD= 2\angle DOE$. 若$\angle BOD= 110^{\circ}$,则$\angle DOE$的度数为______.
答案：
40° 解析因为OB平分∠AOC，所以∠COB=$\frac{1}{2}$∠AOC.因为∠COD=2∠DOE,所以∠COE=3∠DOE.因为∠AOC+∠COE=180°,所以∠AOC=180°−∠COE=180°−3∠DOE.所以∠COB=$\frac{1}{2}$(180°−3∠DOE)=90°−$\frac{3}{2}$∠DOE.因为∠BOD=110°,即∠COB+∠COD=110°,所以90°−$\frac{3}{2}$∠DOE+2∠DOE=110°.所以∠DOE=40°.故答案为40°.
查看更多完整答案，请扫码查看
