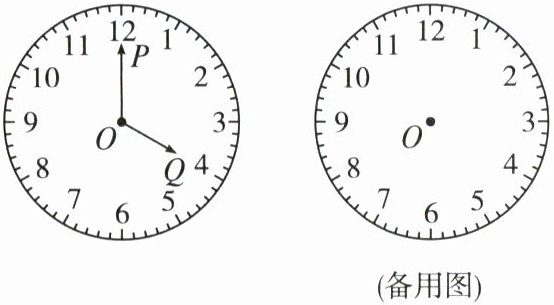
19. 钟表是我们日常生活中常用的计时工具. 如图,在圆形钟面上,把一周等分成 12 个大格,每个大格等分成 5 个小格,分针 $ OP $ 和时针 $ OQ $ 均绕中心 $ O $ 匀速转动.(本题中的角均指小于 $ 180^{\circ} $ 的角)
(1)分针每分钟转______度,时针每分钟转______度. 当时间为 $ 3:30 $ 时,分针和时针的夹角为______度.
(2)求 $ 2:00 $ 开始后几分钟分针第一次追上时针.

(1)分针每分钟转______度,时针每分钟转______度. 当时间为 $ 3:30 $ 时,分针和时针的夹角为______度.
(2)求 $ 2:00 $ 开始后几分钟分针第一次追上时针.
答案:
(1)6 0.5 75 分针每分钟转$\frac{360^{\circ}}{60}=6^{\circ}$,时针每分钟转$\frac{360^{\circ}}{60×12}=0.5^{\circ}$,因为3:30时时针和分针的夹角是2.5个大格,所以3:30时分针和时针的夹角为$30^{\circ}×2.5 = 75^{\circ}$. 故答案为6,0.5,75;
(2)设x分钟后分针第一次追上时针,由题意,得$6x-0.5x = 60$,解得$x=\frac{120}{11}$. 所以$\frac{120}{11}$分钟后分针第一次追上时针.
(1)6 0.5 75 分针每分钟转$\frac{360^{\circ}}{60}=6^{\circ}$,时针每分钟转$\frac{360^{\circ}}{60×12}=0.5^{\circ}$,因为3:30时时针和分针的夹角是2.5个大格,所以3:30时分针和时针的夹角为$30^{\circ}×2.5 = 75^{\circ}$. 故答案为6,0.5,75;
(2)设x分钟后分针第一次追上时针,由题意,得$6x-0.5x = 60$,解得$x=\frac{120}{11}$. 所以$\frac{120}{11}$分钟后分针第一次追上时针.
查看更多完整答案,请扫码查看


