《2025年同步测控优化设计七年级数学上册人教版福建专版》

4. 计算：$4\frac{2}{3}+\frac{1}{5}-12-\frac{6}{5}+6\frac{1}{3}$,阅读解答过程,并按要求解答.
解：原式$=4\frac{2}{3}+\frac{1}{5}+(-12)+(-\frac{6}{5})+6\frac{1}{3}$(第一步)
$=(4\frac{2}{3}+6\frac{1}{3})-(\frac{6}{5}+\frac{1}{5})+(-12)$(第二步)
$=11-\frac{7}{5}+(-12)$(第三步)
$=-1-\frac{7}{5}$(第四步)
$=-2\frac{2}{5}$(第五步)
(1)上面解题过程存在错误,是从第____步开始错误的；
(2)写出正确的解答过程.

答案： （1）二 解析 由题意可得，第二步应该是$(4\frac{2}{3}+6\frac{1}{3})+(-\frac{6}{5}+\frac{1}{5})+(-12)$；
（2）解 原式$=4\frac{2}{3}+\frac{1}{5}+(-12)+(-\frac{6}{5})+6\frac{1}{3}$
$=(4\frac{2}{3}+6\frac{1}{3})+(-\frac{6}{5}+\frac{1}{5})+(-12)$
$=11-1+(-12)=10+(-12)=-2.$

5. 观察前三个图形并找出计算规律,利用同样的计算规律,得到第四个图形的计算结果为( )


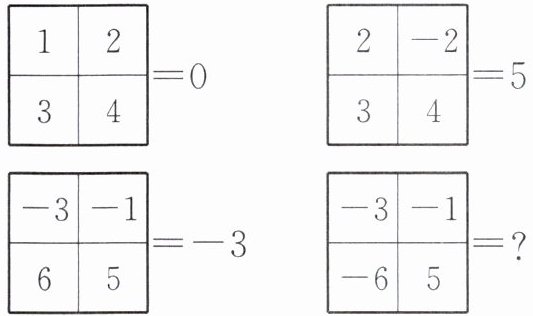
A.$-3$
B.$-5$
C.$5$
D.$9$

答案： D 解析 根据前三个图形得到规律：左上角与右下角的两数之和减去右上角与左下角的两数之和，即可得到答案.
$(1+4)-(2+3)=5-5=0$，
$(2+4)-(-2+3)=6-1=5$，
$(-3+5)-(-1+6)=2-5=-3$，
故$(-3+5)-(-1-6)=2+7=9$.故选D.