《2025年同步练习册青岛出版社六年级数学上册青岛版》

6. 学校对六年级学生观看某频道4档节目的人数统计如下表。
|
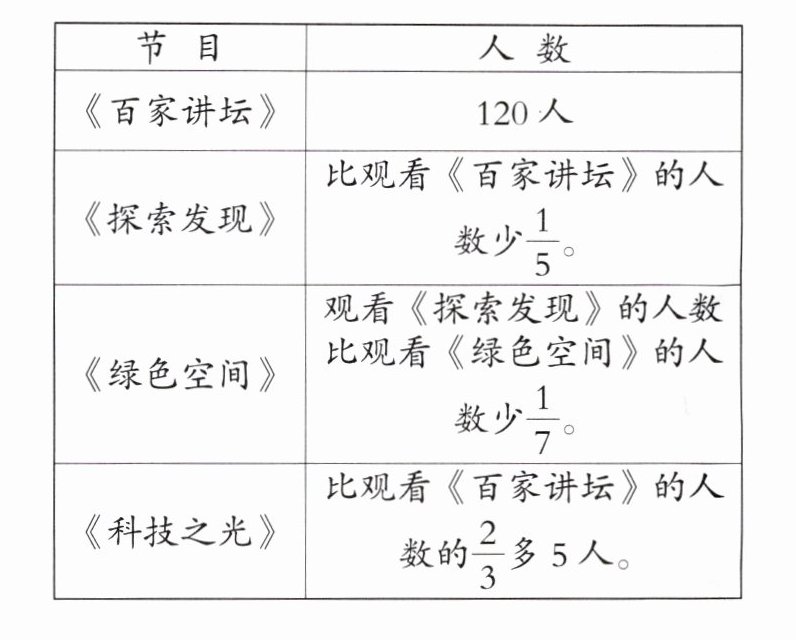
(1)观看《探索发现》的有多少人？
(2)观看《绿色空间》的有多少人？
(3)观看《科技之光》的有多少人？

答案：
(1)120×(1-$\frac{1}{5}$)=120×$\frac{4}{5}$=96(人)
(2)解：设观看《绿色空间》的有x人。
x-$\frac{1}{7}$x=96
$\frac{6}{7}$x=96
x=96÷$\frac{6}{7}$
x=112
(3)120×$\frac{2}{3}$+5=80+5=85(人)

7. 假期里,英子看了一本《上下五千年》,第1天看了20页,第2天看了第1天的$\frac {3}{4}$,两天一共看了这本书的$\frac {5}{6}$。这本书一共有多少页？

答案： 第2天看的页数：$20×\frac{3}{4}=15$（页）
两天一共看的页数：$20 + 15=35$（页）
这本书的总页数：$35÷\frac{5}{6}=35×\frac{6}{5}=42$（页）
答：这本书一共有42页。

8. “村村通”工程实施后,松树村开始铺设村级公路。已铺设的占全长的$\frac {2}{5}$,离中点还有14千米,这条公路全长是多少千米？

答案： 解析：
本题考查的是分数的应用。
设这条公路的全长为$x$千米。
已铺设的公路长度占全长的$\frac{2}{5}$，即已铺设了$\frac{2}{5}x$千米。
同时，离中点还有14千米，即已铺设的长度加上14千米等于公路全长的一半，可以列出方程：
$\frac{2}{5}x+14=\frac{1}{2}x$
将方程两边同时减去$\frac{2}{5}x$，得到：
$14=\frac{1}{2}x-\frac{2}{5}x$
即$14=\frac{1}{10}x$，
解得$x=140$。
所以，这条公路的全长是140千米。
答案：
这条公路的全长是140千米。

9. 一辆汽车从甲地到乙地,行驶到超过中点30千米处时,行了全程的$\frac {4}{5}$,还要行驶多少千米才能到达乙地？

答案： 设甲乙两地全程为$x$千米。
$\frac{4}{5}x - \frac{1}{2}x = 30$
$\frac{8}{10}x - \frac{5}{10}x = 30$
$\frac{3}{10}x = 30$
$x = 30 ÷ \frac{3}{10}$
$x = 100$
$100 × (1 - \frac{4}{5}) = 100 × \frac{1}{5} = 20$（千米）
答：还要行驶20千米才能到达乙地。

10. 学校器材室原有篮球的个数是足球的$\frac {2}{3}$,现在又购进10个篮球,这时篮球个数与足球个数的比是$4:3$,篮球和足球原来各有多少个？

答案： 设足球原来有$x$个，则篮球原来有$\frac{2}{3}x$个。
购进10个篮球后，篮球个数为$\frac{2}{3}x + 10$。
此时篮球个数与足球个数的比是$4:3$，可列方程：
$\frac{\frac{2}{3}x + 10}{x} = \frac{4}{3}$
$3(\frac{2}{3}x + 10) = 4x$
$2x + 30 = 4x$
$4x - 2x = 30$
$2x = 30$
$x = 15$
篮球原来有：$\frac{2}{3}×15 = 10$（个）
答：篮球原来有10个，足球原来有15个。