《2025年同步练习册青岛出版社六年级数学上册青岛版》

(1) 圆规两脚间的距离是 3 厘米,画出的圆的周长是(18.84)厘米,面积是(28.26)平方厘米。

答案： 分析：本题主要考查圆的周长和面积的计算。
圆的周长公式为：$C = 2\pi r$，其中$\pi$取3.14，r为半径。
圆的面积公式为：$S = \pi r^{2}$，其中$\pi$取3.14，r为半径。
已知圆规两脚间的距离是3厘米，即画出的圆的半径$r=3$厘米。
根据圆的周长公式，可计算出圆的周长：
$C = 2\pi r = 2 × 3.14 × 3 = 18.84 \text{(厘米)}$
根据圆的面积公式，可计算出圆的面积：
$S = \pi r^{2} = 3.14 × 3^{2} = 28.26 \text{(平方厘米)}$
答案：18.84；28.26。

(2) 圆的周长是 9.42 分米,它的直径是(3)分米,面积是(7.065)平方分米。

答案： 直径：9.42÷3.14=3(分米)
面积：3.14×(3÷2)²=3.14×2.25=7.065(平方分米)
3；7.065

(3) 将一个直径是 8 厘米的圆形纸片沿直径对折后,得到一个半圆,这个半圆的周长是(20.56)厘米,面积是(25.12)平方厘米。

答案： 半圆的周长：3.14×8÷2 + 8 = 12.56 + 8 = 20.56（厘米）
半圆的面积：3.14×(8÷2)²÷2 = 3.14×16÷2 = 25.12（平方厘米）
20.56，25.12

(4) 小圆半径是大圆半径

的

$\frac {1}{3}$,小圆与大圆的周长比是(1:3),面积比是(1:9)。

答案： 设大圆半径为$r$，则小圆半径为$\frac{1}{3}r$。
小圆周长：$2\pi×\frac{1}{3}r = \frac{2}{3}\pi r$，大圆周长：$2\pi r$，周长比：$\frac{2}{3}\pi r : 2\pi r = 1:3$。
小圆面积：$\pi(\frac{1}{3}r)^2 = \frac{1}{9}\pi r^2$，大圆面积：$\pi r^2$，面积比：$\frac{1}{9}\pi r^2 : \pi r^2 = 1:9$。
1:3，1:9

(5) 甲、乙两圆的周长比是$2:3$,其中甲圆的面积是 18 平方厘米,乙圆的面积是(40.5)平方厘米。

答案： 甲、乙两圆周长比是2:3，所以半径比是2:3。
面积比是半径比的平方，即$2^2:3^2 = 4:9$。
设乙圆面积是$x$平方厘米，可得$4:9 = 18:x$，$4x=18×9$，$4x=162$，$x=40.5$。
40.5

2. 火眼金睛辨对错。
(1) 半圆周长就是圆周长的一半。 (×)
(2) 圆的面积总是它的半径的π倍。 (×)
(3) 圆的半径扩大到原来的 2 倍,直径就扩大到原来的 4 倍。 (×)

答案： 解析：
(1) 半圆的周长包括半圆弧的长度和直径的长度，而圆周长的一半只是半圆弧的长度，所以此说法是错误的。
(2) 圆的面积是$\pi r^2$，而不是$\pi r$，所以此说法是错误的。
(3) 圆的半径扩大到原来的2倍，直径也会扩大到原来的2倍，而不是4倍，所以此说法是错误的。
答案：
(1) ×
(2) ×
(3) ×

(1) 计算圆的面积,可以选择的方法是(D)。
A.$S= πr^{2}$
B.$S= π(d÷2)^{2}$
C.$S= π(C÷2π)^{2}$
D.前 3 种都可以

答案： D

(2) 下面的图形只有两条对称轴的是(A)。
A.长方形
B.正方形
C.等边三角形
D.圆

答案： 解析：本题可根据对称轴的定义，分别分析各选项图形的对称轴数量，进而得出答案。
对称轴是指使几何图形沿着某条直线对折后，直线两侧的部分能够完全重合的直线。
选项A：长方形
长方形沿其对边中点的连线对折后，直线两侧的部分能够完全重合，所以长方形有两条这样的对称轴，即长方形有两条对称轴。
选项B：正方形
正方形沿对边中点的连线对折以及沿两条对角线对折后，直线两侧的部分都能完全重合，所以正方形有四条对称轴。
选项C：等边三角形
等边三角形沿三条高所在的直线对折后，直线两侧的部分都能完全重合，所以等边三角形有三条对称轴。
选项D：圆
圆沿任意一条直径所在的直线对折后，直线两侧的部分都能完全重合，而圆有无数条直径，所以圆有无数条对称轴。
答案：A

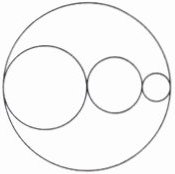
(3) 如图,4 个圆的圆心在同一条直线上,大圆的周长与 3 个小圆的周长之和相比,(C)。

A.大圆的周长长

B.大圆的周长短
C.一样长
D.无法比较

答案： 解析：本题考查圆的周长计算公式的应用。
设大圆的直径为$d_1$，三个小圆的直径分别为$d_{2}、d_{3}、d_{4}$。
根据圆的周长公式$C = \pi d$（其中$C$表示圆的周长，$d$表示圆的直径，$\pi$是一个常数，通常取值3.14 ）。
大圆的周长$C_1 = \pi d_1$。
三个小圆的周长之和$C_2 = \pi d_{2} + \pi d_{3} + \pi d_{4} = \pi (d_{2} + d_{3} + d_{4})$。
由图可知$d_1 = d_{2} + d_{3} + d_{4}$。
所以$C_1 = C_2$，即大圆的周长与三个小圆的周长之和相等。
答案：C。

(4) 一个直径是 1 厘米的圆的面积与一个边长是 1 厘米的正方形的面积相比,(B)。
A.圆的面积大
B.正方形的面积大
C.一样大
D.无法比较

答案： 解析：本题主要考查圆的面积和正方形的面积计算及比较。
首先，计算圆的面积。圆的面积公式是$S = \pi r^{2}$，其中$r$是圆的半径。题目中给出圆的直径是1厘米，所以半径$r = 1 ÷ 2=0.5（厘米）$。代入公式得到圆的面积为$S_{圆} = \pi × (0.5)^{2} = 0.25\pi（平方厘米）$。$\pi$取3.14，得到$S_{圆} =0.25× 3.14= 0.785（平方厘米）$。
接着，计算正方形的面积。正方形的面积公式是$S = a^{2}$，其中$a$是正方形的边长。题目中给出正方形的边长是1厘米，代入公式得到正方形的面积为$S_{正方形} = 1^{2} = 1（平方厘米）$。
最后，比较两者的面积。由于$0.785 \lt 1$，即$S_{圆} \lt S_{正方形}$，所以正方形的面积大。
答案：B。