《2025年同步练习册青岛出版社六年级数学上册青岛版》

7. (1)如下图,给饭桌铺上和桌面同样大小的水晶板,水晶板的面积是多少平方米?

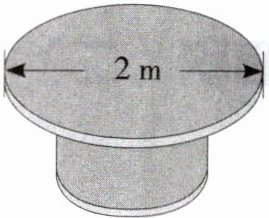
(2)为了美观,要在水晶板的周围镶上花边,至少需要多长的花边?

答案：
(1)水晶板的面积：$3.14×(2÷2)^2 = 3.14×1 = 3.14$（平方米）
(2)花边长度：$3.14×2 = 6.28$（米）

8. 南湖公园修了一个圆形水池,水池的周长为50.24米,它的占地面积是多少平方米?

答案： 解析：本题考查圆的周长和面积公式的应用。
首先，根据圆的周长公式$C = 2\pi r$，其中C是周长，r是半径，$\pi$取3.14，可得：
$r = \frac{C}{2\pi} = \frac{50.24}{2 × 3.14} = 8$（米），
然后，根据圆的面积公式$S = \pi r^{2}$，其中S是面积，可得：
$S = 3.14 × 8^{2} = 200.96$（平方米）。
答案：200.96平方米。

9. 在一块长方形的空地上修一个最大的圆形花坛(如下图),其余部分种草。草坪的占地面积是多少平方米?

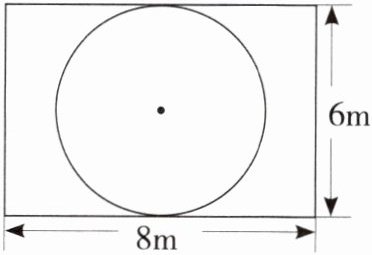
答案： 长方形面积：8×6=48（平方米）
圆的半径：6÷2=3（米）
圆的面积：3.14×3²=28.26（平方米）
草坪面积：48-28.26=19.74（平方米）
答：草坪的占地面积是19.74平方米。

10. 一个钟表的分针长15厘米,时针长8厘米。时针和分针各走一圈,它们扫过的面积相差多少平方厘米?

答案： 3.14×15² - 3.14×8²
=3.14×225 - 3.14×64
=706.5 - 200.96
=505.54（平方厘米）
答：它们扫过的面积相差505.54平方厘米。

11. 刘徽割圆术。
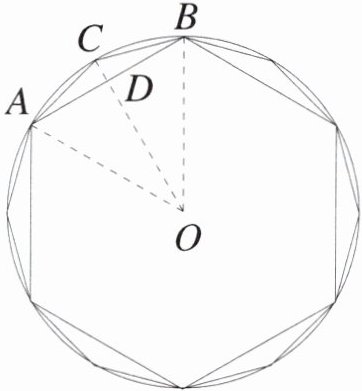
3世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了完善的理论和严密的算法。“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。”这就是说,圆内接正多边形的边数无限增加的时候,它的周长的极限就是圆周长,它的面积的极限就是圆面积。
你能结合刘徽的割圆术,根据圆周长的计算公式推导出圆面积的计算公式吗?赶紧动手试试吧!

答案： 将圆等分成n个小扇形，每个扇形可近似看作三角形，其半径为圆的半径r，底边长近似为圆周长的n分之一，即底边长≈C/n。每个小三角形的面积≈(底×高)/2=(C/n×r)/2。圆的面积近似等于n个小三角形面积之和，即S≈n×(C/n×r)/2= (C×r)/2。因为圆周长C=2πr，所以S=(2πr×r)/2=πr²。
结论：圆面积计算公式为S=πr²。