《2025年同步练习册青岛出版社六年级数学上册青岛版》

7. 小军早上绕学校操场(如下图)跑了5圈,一共跑了多少米?

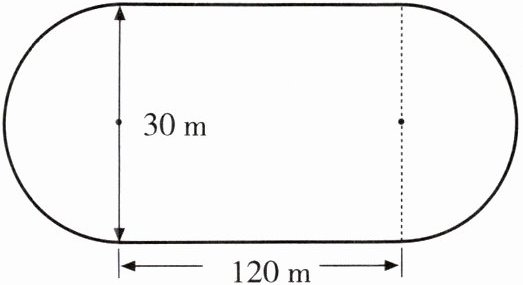
答案： 操场周长：$3.14×30 + 120×2 = 94.2 + 240 = 334.2$（米）
总路程：$334.2×5 = 1671$（米）
答：一共跑了1671米。

8. 游乐场新建了一个圆形花坛,直径是50米。在这个花坛的周围每隔1米栽一棵树,可以栽多少棵?

答案： 圆形花坛的周长：$C = \pi d = 3.14×50 = 157$（米）
可栽树的棵数：$157÷1 = 157$（棵）
答：可以栽157棵。

9. 一个羊圈依墙而建,呈半圆形,半径是9米。
(1) 修这个羊圈需要多少米篱笆?

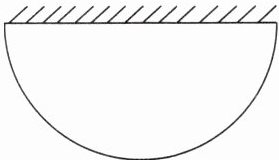
(2) 如果要扩建这个羊圈,把它的半径增加1米,需要增加多少米篱笆?

答案：
(1) 3.14×9×2÷2=28.26(米)
(2) 3.14×(9+1)×2÷2 - 28.26=3.14(米)

10. 为方便销售,售货员把啤酒捆成如下图(从瓶底方向看)的形状,把4个直径为6cm的圆柱形酒瓶捆扎5圈,如果绳子接头处不计,需要多长的绳子?

答案： 一圈绳子长度：$3.14×6 + 6×4 = 18.84 + 24 = 42.84$（cm）
总长度：$42.84×5 = 214.2$（cm）
答：需要214.2厘米长的绳子。

11. 如图,从点M到点N有两条路可走,你认为哪条路更近一些?请通过计算说明理由。

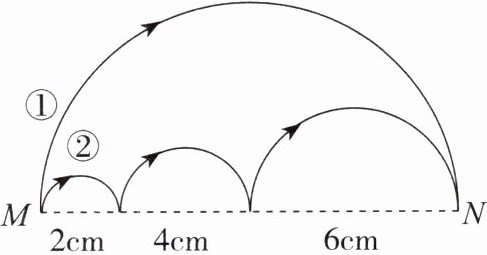
答案： 本题可分别计算出两条路的长度，再对二者进行比较，从而判断哪条路更近。
步骤一：分析两条路的组成并分别计算其长度
路线①：
观察图形可知，路线①是一个大半圆的弧长。
已知该大半圆的直径为$2 + 4 + 6 = 12cm$，根据圆的周长公式$C = \pi d$（其中$C$表示圆的周长，$d$表示圆的直径，$\pi$通常取$3.14$），那么该大半圆的弧长为圆周长的一半，即$\dfrac{1}{2}×\pi×(2 + 4 + 6)=\dfrac{1}{2}×\pi×12 = 6\pi cm$。
路线②：
路线②由三个小半圆的弧长组成，这三个小半圆的直径分别为$2cm$、$4cm$、$6cm$。
根据圆的周长公式，分别计算三个小半圆的弧长：
直径为$2cm$的小半圆的弧长为$\dfrac{1}{2}×\pi×2=\pi cm$；
直径为$4cm$的小半圆的弧长为$\dfrac{1}{2}×\pi×4 = 2\pi cm$；
直径为$6cm$的小半圆的弧长为$\dfrac{1}{2}×\pi×6 = 3\pi cm$。
将三个小半圆的弧长相加，可得路线②的长度为$\pi + 2\pi + 3\pi = 6\pi cm$。
步骤二：比较两条路的长度
由上述计算可知，路线①的长度为$6\pi cm$，路线②的长度也为$6\pi cm$，因为$6\pi = 6\pi$，所以两条路一样近。
综上，两条路一样近，理由是路线①的长度为$6\pi cm$，路线②的长度也为$6\pi cm$。

12. 读材料,解答问题。
赤道是地球表面的点随地球自转产生的轨迹中周长最长的圆周线,是一个近似的圆形。如果把赤道看作一个以地心为圆心的圆,那么可以说它是地球上最大的圆了。
赤道的半径大约是6378千米,它的周长大约是多少千米? (结果精确到万位。)

答案： C=2πr=2×3.14×6378=40053.84（千米）≈4万千米
答：它的周长大约是4万千米。