4. 一个平行四边形,高为$\frac{4}{5}$m,它的底是高的$\frac{3}{4}$,这个平行四边形的面积为(
A.$\frac{3}{5}$m^2
B.$\frac{9}{25}$m^2
C.$\frac{12}{25}$m^2
C
)。A.$\frac{3}{5}$m^2
B.$\frac{9}{25}$m^2
C.$\frac{12}{25}$m^2
答案:
C
1. 一个非0自然数乘一个真分数,积一定比这个数小。 (
√
)
答案:
√
2. 4m的$\frac{1}{5}$和5m的$\frac{1}{4}$一样长。 (
×
)
答案:
×
3. $\frac{2}{3}乘\frac{3}{4}的积在\frac{3}{4}和\frac{1}{3}$之间。 (
√
)
答案:
√
4. 若甲的$\frac{3}{4}等于乙的\frac{2}{3}$,则甲>乙。 (
×
)
答案:
×
5. 5kg苹果,吃掉$\frac{4}{5}$kg后,还剩下1kg苹果。 (
×
)
答案:
×
四、我会算。(怎样简便怎样算)
$\frac{7}{9}×\frac{15}{11}-\frac{7}{9}×\frac{4}{11}$ $24×(\frac{7}{8}-\frac{5}{12})$ $(\frac{7}{13}×34)×(13×\frac{3}{17})$
$\frac{12}{19}×2+\frac{12}{19}×\frac{5}{7}$ $\frac{8}{27}×28$ $\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}$
$\frac{7}{9}×\frac{15}{11}-\frac{7}{9}×\frac{4}{11}$ $24×(\frac{7}{8}-\frac{5}{12})$ $(\frac{7}{13}×34)×(13×\frac{3}{17})$
$\frac{12}{19}×2+\frac{12}{19}×\frac{5}{7}$ $\frac{8}{27}×28$ $\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}$
答案:
1. 计算$\frac{7}{9}×\frac{15}{11}-\frac{7}{9}×\frac{4}{11}$:
解:根据乘法分配律$a× c - b× c=(a - b)× c$,这里$a = \frac{15}{11}$,$b=\frac{4}{11}$,$c=\frac{7}{9}$。
$\frac{7}{9}×\frac{15}{11}-\frac{7}{9}×\frac{4}{11}=\frac{7}{9}×(\frac{15}{11}-\frac{4}{11})$
$=\frac{7}{9}×\frac{15 - 4}{11}$
$=\frac{7}{9}×1$
$=\frac{7}{9}$。
2. 计算$24×(\frac{7}{8}-\frac{5}{12})$:
解:根据乘法分配律$a×(b - c)=a× b-a× c$,这里$a = 24$,$b=\frac{7}{8}$,$c=\frac{5}{12}$。
$24×(\frac{7}{8}-\frac{5}{12})=24×\frac{7}{8}-24×\frac{5}{12}$
$=3×7 - 2×5$
$=21 - 10$
$=11$。
3. 计算$(\frac{7}{13}×34)×(13×\frac{3}{17})$:
解:根据乘法交换律$a× b=b× a$和结合律$(a× b)× c=a×(b× c)$。
$(\frac{7}{13}×34)×(13×\frac{3}{17})=(\frac{7}{13}×13)×(34×\frac{3}{17})$
$=7×(2×3)$
$=7×6$
$=42$。
4. 计算$\frac{12}{19}×2+\frac{12}{19}×5$:
解:根据乘法分配律$a× c + b× c=(a + b)× c$,这里$a = 2$,$b = 5$,$c=\frac{12}{19}$。
$\frac{12}{19}×2+\frac{12}{19}×5=\frac{12}{19}×(2 + 5)$
$=\frac{12}{19}×7$
$=\frac{84}{19}$。
5. 计算$\frac{8}{27}×28$:
解:把$28$写成$(27 + 1)$,再根据乘法分配律$a×(b + c)=a× b+a× c$,这里$a=\frac{8}{27}$,$b = 27$,$c = 1$。
$\frac{8}{27}×28=\frac{8}{27}×(27+1)$
$=\frac{8}{27}×27+\frac{8}{27}×1$
$=8+\frac{8}{27}$
$=8\frac{8}{27}$。
6. 计算$\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}$:
解:根据加法交换律$a + b=b + a$和结合律$(a + b)+c=a+(b + c)$。
$\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}=(\frac{4}{7}-\frac{4}{7})+(\frac{3}{5}+\frac{2}{5})$
$=0 + 1$
$=1$。
综上,答案依次为$\frac{7}{9}$;$11$;$42$;$\frac{84}{19}$;$8\frac{8}{27}$;$1$。
解:根据乘法分配律$a× c - b× c=(a - b)× c$,这里$a = \frac{15}{11}$,$b=\frac{4}{11}$,$c=\frac{7}{9}$。
$\frac{7}{9}×\frac{15}{11}-\frac{7}{9}×\frac{4}{11}=\frac{7}{9}×(\frac{15}{11}-\frac{4}{11})$
$=\frac{7}{9}×\frac{15 - 4}{11}$
$=\frac{7}{9}×1$
$=\frac{7}{9}$。
2. 计算$24×(\frac{7}{8}-\frac{5}{12})$:
解:根据乘法分配律$a×(b - c)=a× b-a× c$,这里$a = 24$,$b=\frac{7}{8}$,$c=\frac{5}{12}$。
$24×(\frac{7}{8}-\frac{5}{12})=24×\frac{7}{8}-24×\frac{5}{12}$
$=3×7 - 2×5$
$=21 - 10$
$=11$。
3. 计算$(\frac{7}{13}×34)×(13×\frac{3}{17})$:
解:根据乘法交换律$a× b=b× a$和结合律$(a× b)× c=a×(b× c)$。
$(\frac{7}{13}×34)×(13×\frac{3}{17})=(\frac{7}{13}×13)×(34×\frac{3}{17})$
$=7×(2×3)$
$=7×6$
$=42$。
4. 计算$\frac{12}{19}×2+\frac{12}{19}×5$:
解:根据乘法分配律$a× c + b× c=(a + b)× c$,这里$a = 2$,$b = 5$,$c=\frac{12}{19}$。
$\frac{12}{19}×2+\frac{12}{19}×5=\frac{12}{19}×(2 + 5)$
$=\frac{12}{19}×7$
$=\frac{84}{19}$。
5. 计算$\frac{8}{27}×28$:
解:把$28$写成$(27 + 1)$,再根据乘法分配律$a×(b + c)=a× b+a× c$,这里$a=\frac{8}{27}$,$b = 27$,$c = 1$。
$\frac{8}{27}×28=\frac{8}{27}×(27+1)$
$=\frac{8}{27}×27+\frac{8}{27}×1$
$=8+\frac{8}{27}$
$=8\frac{8}{27}$。
6. 计算$\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}$:
解:根据加法交换律$a + b=b + a$和结合律$(a + b)+c=a+(b + c)$。
$\frac{4}{7}+\frac{3}{5}-\frac{4}{7}+\frac{2}{5}=(\frac{4}{7}-\frac{4}{7})+(\frac{3}{5}+\frac{2}{5})$
$=0 + 1$
$=1$。
综上,答案依次为$\frac{7}{9}$;$11$;$42$;$\frac{84}{19}$;$8\frac{8}{27}$;$1$。
五、我能看图列式并计算。
1. 2.

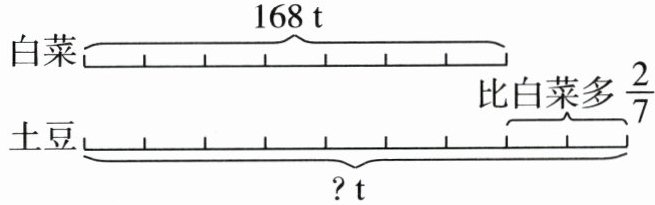
1. 2.


答案:
1.$150× \left(1-\frac{2}{5}\right)=90$(页) 2.$168× \left(1+\frac{2}{7}\right)=216$(t)
查看更多完整答案,请扫码查看


