《2025年教材课本六年级数学上册苏教版》

2 在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球？每个小盒呢？

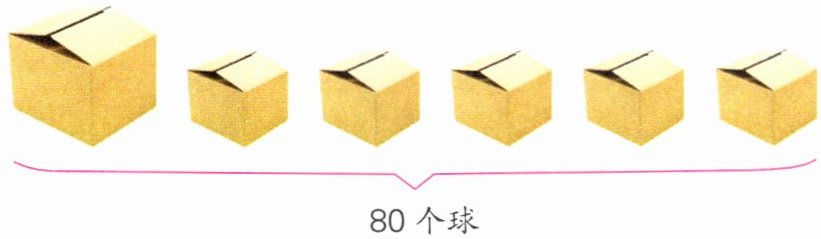
80个球
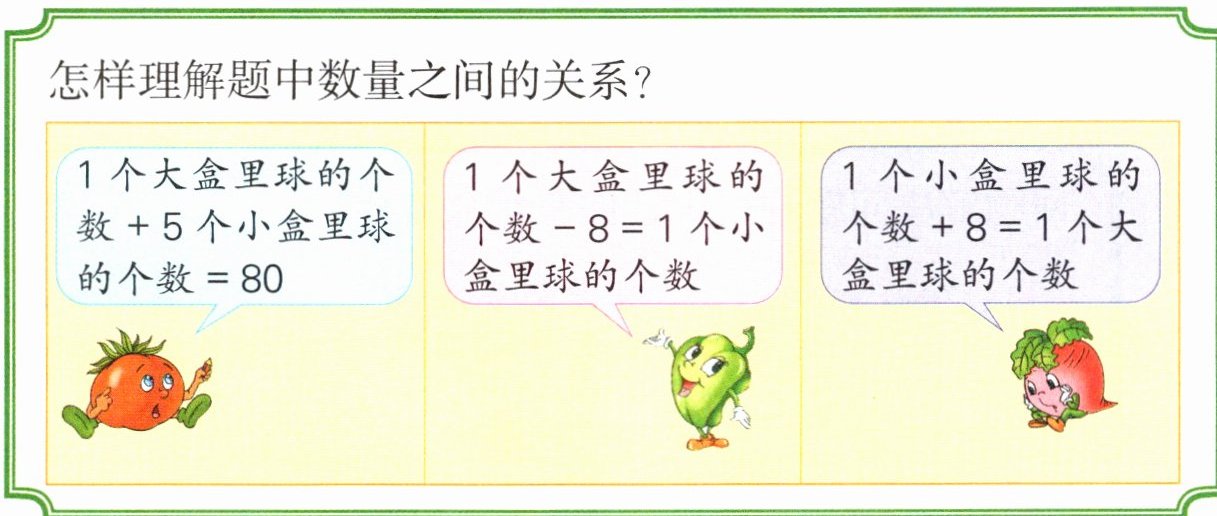
怎样理解题中数量之间的关系？
1个大盒里球的个数+5个小盒里球的个数= 80
1个大盒里球的个数-8= 1个小盒里球的个数
1个小盒里球的个数+8= 1个大盒里球的个数

假设6个全是小盒,球的总数会发生什么变化？
假设6个全是小盒,也就是把1个大盒换成小盒。
6个全是小盒,球的总数比80少。
把1个大盒换成小盒,球的总数要比80少8。
先根据假设后的数量关系列式解答,再进行检验。
答：大盒里装了____个,每个小盒装了____个。
回顾例1和例2解决问题的过程,你有什么体会？
都可以通过假设使数量关系变得简单。
要弄清假设前后的数量关系,注意假设前后总量有没有变化。
要在不同的假设方法中选择比较简单的。

答案： 假设6个全是小盒，球的总数比80少8个。
小盒：(80-8)÷6=12(个)
大盒：12+8=20(个)
检验：20+5×12=80(个)，20-12=8(个)，符合题意。
答：大盒里装了20个，每个小盒装了12个。