第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
四 解决问题的策略
1 小明把720毫升果汁倒入6个小杯和1个大杯,正好都倒满。已知小杯的容量是大杯的$\frac{1}{3}$,小杯和大杯的容量各是多少毫升?
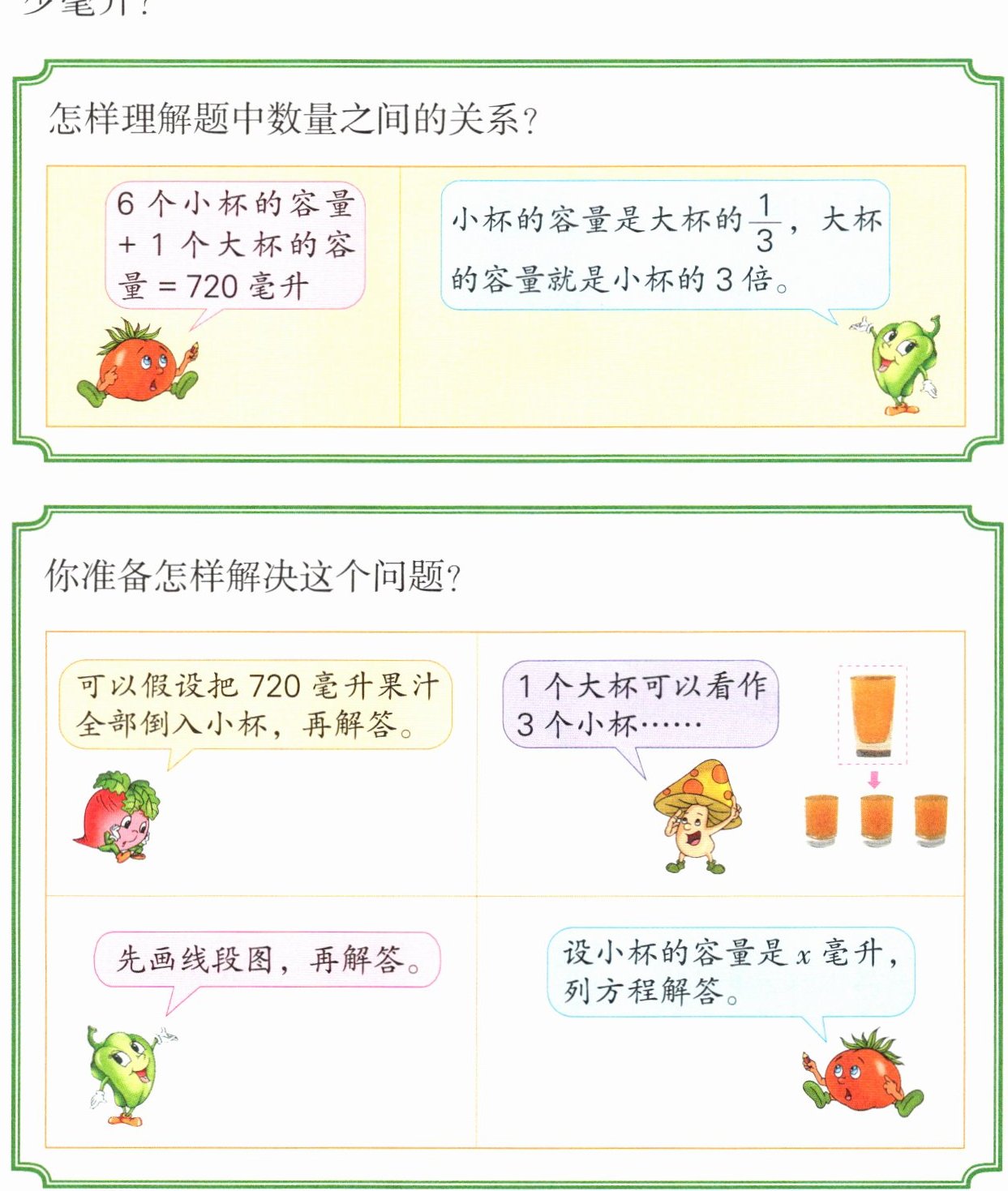
怎样理解题中数量之间的关系?
6个小杯的容量+1个大杯的容量= 720毫升
小杯的容量是大杯的$\frac{1}{3}$,大杯的容量就是小杯的3倍。
你准备怎样解决这个问题?
可以假设把720毫升果汁全部倒入小杯,再解答。
1个大杯可以看作3个小杯……
先画线段图,再解答。
设小杯的容量是x毫升,列方程解答。
选择一种方法列式解答,并进行检验。
答:小杯的容量是____毫升,大杯的容量是____毫升。
想一想:假设把720毫升果汁全部倒入大杯,可以倒满几个大杯?你能根据这样的假设算出结果吗?
回顾解决问题的过程,你有什么体会?
通过假设可以转化问题,使数量关系变得简单。
假设时要弄清楚数量之间的关系。
假设时也可以用字母表示未知量,列方程解答。

在以前的学习中,我们曾经运用假设的策略解决过哪些问题?
计算除数是两位数的除法,把除数当作整十数试商。
把接近整百或整十的数看作整百或整十数,估算出大致的结果。
已知两个数的和与差,假设两个数同样多,分别求出这两个数。

1 小明把720毫升果汁倒入6个小杯和1个大杯,正好都倒满。已知小杯的容量是大杯的$\frac{1}{3}$,小杯和大杯的容量各是多少毫升?

怎样理解题中数量之间的关系?
6个小杯的容量+1个大杯的容量= 720毫升
小杯的容量是大杯的$\frac{1}{3}$,大杯的容量就是小杯的3倍。
你准备怎样解决这个问题?
可以假设把720毫升果汁全部倒入小杯,再解答。
1个大杯可以看作3个小杯……
先画线段图,再解答。
设小杯的容量是x毫升,列方程解答。
选择一种方法列式解答,并进行检验。
答:小杯的容量是____毫升,大杯的容量是____毫升。
想一想:假设把720毫升果汁全部倒入大杯,可以倒满几个大杯?你能根据这样的假设算出结果吗?
回顾解决问题的过程,你有什么体会?
通过假设可以转化问题,使数量关系变得简单。
假设时要弄清楚数量之间的关系。
假设时也可以用字母表示未知量,列方程解答。

在以前的学习中,我们曾经运用假设的策略解决过哪些问题?
计算除数是两位数的除法,把除数当作整十数试商。
把接近整百或整十的数看作整百或整十数,估算出大致的结果。
已知两个数的和与差,假设两个数同样多,分别求出这两个数。

答案:
假设把720毫升果汁全部倒入小杯,1个大杯相当于3个小杯,那么一共有小杯:6 + 3 = 9(个)
小杯容量:720 ÷ 9 = 80(毫升)
大杯容量:80 × 3 = 240(毫升)
检验:6×80 + 240 = 480 + 240 = 720(毫升),且80÷240 = 1/3,符合题意。
答:小杯的容量是80毫升,大杯的容量是240毫升。
想一想:6个小杯相当于6÷3 = 2个大杯,全部倒入大杯可倒满2 + 1 = 3个大杯。大杯容量:720÷3 = 240(毫升),小杯容量:240×1/3 = 80(毫升)。
小杯容量:720 ÷ 9 = 80(毫升)
大杯容量:80 × 3 = 240(毫升)
检验:6×80 + 240 = 480 + 240 = 720(毫升),且80÷240 = 1/3,符合题意。
答:小杯的容量是80毫升,大杯的容量是240毫升。
想一想:6个小杯相当于6÷3 = 2个大杯,全部倒入大杯可倒满2 + 1 = 3个大杯。大杯容量:720÷3 = 240(毫升),小杯容量:240×1/3 = 80(毫升)。
查看更多完整答案,请扫码查看


