第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
5. 右边的长方体和正方体都是用棱长1厘米的正方体摆成的。它们的表面积和体积各是多少?
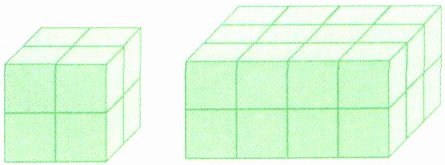

答案:
长方体
表面积:$(4×2 + 4×2 + 2×2)×2$
$=(8 + 8 + 4)×2$
$=20×2$
$=40$(平方厘米)
体积:$4×2×2 = 16$(立方厘米)
正方体
表面积:$2×2×6 = 24$(平方厘米)
体积:$2×2×2 = 8$(立方厘米)
结论:长方体表面积40平方厘米,体积16立方厘米;正方体表面积24平方厘米,体积8立方厘米。
表面积:$(4×2 + 4×2 + 2×2)×2$
$=(8 + 8 + 4)×2$
$=20×2$
$=40$(平方厘米)
体积:$4×2×2 = 16$(立方厘米)
正方体
表面积:$2×2×6 = 24$(平方厘米)
体积:$2×2×2 = 8$(立方厘米)
结论:长方体表面积40平方厘米,体积16立方厘米;正方体表面积24平方厘米,体积8立方厘米。
6. 下面是长方体和正方体的表面展开图,你能先测量,再分别算出它们的表面积和体积吗?


答案:
本题可先通过测量长方体和正方体展开图相关棱长的长度,再根据长方体和正方体的表面积及体积公式分别计算它们的表面积和体积。
步骤一:测量长方体展开图相关棱长
假设测量得到长方体展开图中长为$4$厘米,宽为$3$厘米,高为$2$厘米。
步骤二:计算长方体的表面积和体积
计算长方体的表面积:
长方体的表面积公式为$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高)。
将$a = 4$厘米,$b = 3$厘米,$h = 2$厘米代入公式可得:
$\begin{aligned}S&=(4×3 + 4×2 + 3×2)×2\\&=(12 + 8 + 6)×2\\&=(20 + 6)×2\\&= 26×2\\&= 52(平方厘米)\end{aligned}$
计算长方体的体积:
长方体的体积公式为$V = abh$。
将$a = 4$厘米,$b = 3$厘米,$h = 2$厘米代入公式可得:
$V = 4×3×2 = 24$(立方厘米)
步骤三:测量正方体展开图相关棱长
假设测量得到正方体展开图中棱长为$3$厘米。
步骤四:计算正方体的表面积和体积
计算正方体的表面积:
正方体的表面积公式为$S = 6a^2$(其中$a$为棱长)。
将$a = 3$厘米代入公式可得:
$S = 6×3^2 = 6×9 = 54$(平方厘米)
计算正方体的体积:
正方体的体积公式为$V = a^3$。
将$a = 3$厘米代入公式可得:
$V = 3^3 = 27$(立方厘米)
综上,长方体的表面积是$52$平方厘米,体积是$24$立方厘米;正方体的表面积是$54$平方厘米,体积是$27$立方厘米。
步骤一:测量长方体展开图相关棱长
假设测量得到长方体展开图中长为$4$厘米,宽为$3$厘米,高为$2$厘米。
步骤二:计算长方体的表面积和体积
计算长方体的表面积:
长方体的表面积公式为$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高)。
将$a = 4$厘米,$b = 3$厘米,$h = 2$厘米代入公式可得:
$\begin{aligned}S&=(4×3 + 4×2 + 3×2)×2\\&=(12 + 8 + 6)×2\\&=(20 + 6)×2\\&= 26×2\\&= 52(平方厘米)\end{aligned}$
计算长方体的体积:
长方体的体积公式为$V = abh$。
将$a = 4$厘米,$b = 3$厘米,$h = 2$厘米代入公式可得:
$V = 4×3×2 = 24$(立方厘米)
步骤三:测量正方体展开图相关棱长
假设测量得到正方体展开图中棱长为$3$厘米。
步骤四:计算正方体的表面积和体积
计算正方体的表面积:
正方体的表面积公式为$S = 6a^2$(其中$a$为棱长)。
将$a = 3$厘米代入公式可得:
$S = 6×3^2 = 6×9 = 54$(平方厘米)
计算正方体的体积:
正方体的体积公式为$V = a^3$。
将$a = 3$厘米代入公式可得:
$V = 3^3 = 27$(立方厘米)
综上,长方体的表面积是$52$平方厘米,体积是$24$立方厘米;正方体的表面积是$54$平方厘米,体积是$27$立方厘米。
7. 有一个花坛,高0.5米,底面是边长1.3米的正方形。四周用砖砌成,砖墙的厚度是0.3米,中间填满泥土。
(1)花坛所占的空间有多大?
(2)花坛里大约有泥土多少立方米?
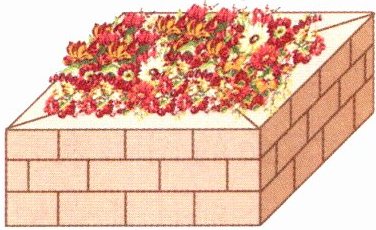
(1)花坛所占的空间有多大?
(2)花坛里大约有泥土多少立方米?

答案:
解析:本题考查长方体体积的计算。
(1)求花坛所占的空间有多大,就是求这个长方体的体积,根据长方体的体积公式:$V = a × b × h$,其中$V$表示体积,$a$表示长,$b$表示宽,$h$表示高。
已知花坛底面是边长$1.3$米的正方形,高$0.5$米,将数值代入公式可得:
$V=1.3×1.3×0.5$
$=1.69×0.5$
$ = 0.845$(立方米)
(2)求花坛里大约有泥土多少立方米,需要先求出填泥土部分的底面边长,再用长方体体积公式计算。
已知底面是边长$1.3$米的正方形,砖墙的厚度是$0.3$米,那么填泥土部分的底面边长为:
$1.3 - 0.3×2$
$=1.3 - 0.6$
$= 0.7$(米)
高为$0.5$米,根据长方体体积公式可得泥土的体积为:
$V = 0.7×0.7×0.5$
$=0.49×0.5$
$ = 0.245$(立方米)
答案:
(1)$1.3×1.3×0.5 = 0.845$(立方米)
答:花坛所占的空间是$0.845$立方米。
(2)$(1.3 - 0.3×2)×(1.3 - 0.3×2)×0.5 = 0.245$(立方米)
答:花坛里大约有泥土$0.245$立方米。
(1)求花坛所占的空间有多大,就是求这个长方体的体积,根据长方体的体积公式:$V = a × b × h$,其中$V$表示体积,$a$表示长,$b$表示宽,$h$表示高。
已知花坛底面是边长$1.3$米的正方形,高$0.5$米,将数值代入公式可得:
$V=1.3×1.3×0.5$
$=1.69×0.5$
$ = 0.845$(立方米)
(2)求花坛里大约有泥土多少立方米,需要先求出填泥土部分的底面边长,再用长方体体积公式计算。
已知底面是边长$1.3$米的正方形,砖墙的厚度是$0.3$米,那么填泥土部分的底面边长为:
$1.3 - 0.3×2$
$=1.3 - 0.6$
$= 0.7$(米)
高为$0.5$米,根据长方体体积公式可得泥土的体积为:
$V = 0.7×0.7×0.5$
$=0.49×0.5$
$ = 0.245$(立方米)
答案:
(1)$1.3×1.3×0.5 = 0.845$(立方米)
答:花坛所占的空间是$0.845$立方米。
(2)$(1.3 - 0.3×2)×(1.3 - 0.3×2)×0.5 = 0.245$(立方米)
答:花坛里大约有泥土$0.245$立方米。
8. 一种长方体的广告灯箱,框架由铝合金条制成,各个面都用灯箱布围成。制作一个这样的广告灯箱,至少需要铝合金条多少分米?需要灯箱布多少平方分米?


答案:
解析:本题考查长方体棱长总和以及表面积的计算。
长方体棱长总和公式为$L = 4×(a + b + h)$(其中$a$为长,$b$为宽,$h$为高)。
长方体表面积公式为$S = 2×(ab + bh + ah)$。
已知长方体广告灯箱的长$a = 70cm$,宽$b = 15cm$,高$h = 120cm$。
求需要铝合金条的长度,即求长方体的棱长总和:
$\;\;\;\;4×(70 + 15 + 120)$
$= 4×205$
$= 820$($cm$)
因为$1dm=10cm$,所以$820cm=82dm$。
求需要灯箱布的面积,即求长方体的表面积:
$\;\;\;\;2×(70×15 + 70×120 + 15×120)$
$= 2×(1050 + 8400 + 1800)$
$= 2×11250$
$= 22500$($cm^2$)
因为$1dm^2 = 100cm^2$,所以$22500cm^2 = 225dm^2$。
答案:至少需要铝合金条$82dm$,需要灯箱布$225dm^2$。
长方体棱长总和公式为$L = 4×(a + b + h)$(其中$a$为长,$b$为宽,$h$为高)。
长方体表面积公式为$S = 2×(ab + bh + ah)$。
已知长方体广告灯箱的长$a = 70cm$,宽$b = 15cm$,高$h = 120cm$。
求需要铝合金条的长度,即求长方体的棱长总和:
$\;\;\;\;4×(70 + 15 + 120)$
$= 4×205$
$= 820$($cm$)
因为$1dm=10cm$,所以$820cm=82dm$。
求需要灯箱布的面积,即求长方体的表面积:
$\;\;\;\;2×(70×15 + 70×120 + 15×120)$
$= 2×(1050 + 8400 + 1800)$
$= 2×11250$
$= 22500$($cm^2$)
因为$1dm^2 = 100cm^2$,所以$22500cm^2 = 225dm^2$。
答案:至少需要铝合金条$82dm$,需要灯箱布$225dm^2$。
9. 一种正方体的工艺蜡烛盒,四周和底面都是玻璃,棱长6厘米。这个蜡烛盒的体积是多少立方厘米?做这个蜡烛盒至少要用多少玻璃?


答案:
体积:6×6×6=216(立方厘米)
玻璃面积:6×6×5=180(平方厘米)
答:这个蜡烛盒的体积是216立方厘米,做这个蜡烛盒至少要用180平方厘米玻璃。
玻璃面积:6×6×5=180(平方厘米)
答:这个蜡烛盒的体积是216立方厘米,做这个蜡烛盒至少要用180平方厘米玻璃。
10. 一件雕塑的底座是用混凝土浇筑成的棱长2.6米的正方体。
(1)这件雕塑的底座占地多少平方米?
(2)浇筑这件雕塑的底座需要混凝土多少立方米?
(3)给底座四面贴上花岗石,贴花岗石的面积是多少平方米?
(1)这件雕塑的底座占地多少平方米?
(2)浇筑这件雕塑的底座需要混凝土多少立方米?
(3)给底座四面贴上花岗石,贴花岗石的面积是多少平方米?
答案:
解析:
本题主要考察正方体的面积和体积计算。
(1) 雕塑底座占地的面积即为正方体的底面积。
(2) 浇筑底座需要的混凝土体积即为正方体的体积。
(3) 贴花岗石的面积为正方体的四个侧面的面积总和。
答案:
(1)底座占地面积 = $2.6 × 2.6 = 6.76$(平方米)
答:这件雕塑的底座占地6.76平方米。
(2)需要混凝土的体积 = $2.6 × 2.6 × 2.6 = 17.576$(立方米)
答:浇筑这件雕塑的底座需要混凝土17.576立方米。
(3)贴花岗石的面积 = $2.6 × 2.6 × 4 = 27.04$(平方米)
答:给底座四面贴上花岗石,贴花岗石的面积是27.04平方米。
本题主要考察正方体的面积和体积计算。
(1) 雕塑底座占地的面积即为正方体的底面积。
(2) 浇筑底座需要的混凝土体积即为正方体的体积。
(3) 贴花岗石的面积为正方体的四个侧面的面积总和。
答案:
(1)底座占地面积 = $2.6 × 2.6 = 6.76$(平方米)
答:这件雕塑的底座占地6.76平方米。
(2)需要混凝土的体积 = $2.6 × 2.6 × 2.6 = 17.576$(立方米)
答:浇筑这件雕塑的底座需要混凝土17.576立方米。
(3)贴花岗石的面积 = $2.6 × 2.6 × 4 = 27.04$(平方米)
答:给底座四面贴上花岗石,贴花岗石的面积是27.04平方米。
查看更多完整答案,请扫码查看


