《2025年顶尖课课练九年级数学上册人教版》

2. 给出下列命题：①直径是弦；②长度相等的两条弧是等弧；③直径相等的两个圆是等圆；④半径相等的两个半圆是等弧；⑤只有在同圆或等圆中，才会存在等弧.其中正确的是①③④⑤\_\_\_\_\_\_.（填序号）

答案： ①③④⑤

3. 已知 $\odot O$ 的直径 $ AB = 6\mathrm \,{cm}$，则圆上任意一点到圆心的距离是(B).

A.$ 2\mathrm \,{cm} $
B.$ 3\mathrm \,{cm} $
C.$ 6\mathrm \,{cm} $
D.不确定的

答案： B

4. 如图 $ 24.1.1 - 1 $，已知 $ AB $ 是 $\odot O$ 的直径，点 $ C $ 在 $\odot O$ 上，点 $ D $ 是 $ BC $ 的中点.若 $ AC = 10\mathrm \,{cm} $，则 $ OD = \_\_\_\_\_\_\mathrm5\,{cm} $.

答案： 5

5. 若一个点到圆上的最小距离是$ 4\mathrm \,{cm} ，$最大距离是$ 9\mathrm \,{cm} ，$则圆的半径是$ \_\_\_\_\_\_\mathrm2.5 或 6.5\,{cm} .$

答案： 2.5 或 6.5

6. 如图 $ 24.1.1 - 2 $，已知 $ BC $ 是 $\odot O$ 的直径，半径 $ OA \perp BC $，点 $ D $ 在劣弧 $ AC $ 上(不与点 $ A $，$ C $ 重合)，$ BD $ 与 $ OA $ 交于点 $ E $.设 $ \angle AED = \alpha $，$ \angle AOD = \beta $，则(D).

A.$ 3\alpha + \beta = 180° $
B.$ 2\alpha + \beta = 180° $
C.$ 3\alpha - \beta = 90° $
D.$ 2\alpha - \beta = 90° $

答案： D

7. 如图 $ 24.1.1 - 3 $，弧 $ AD $ 是以等边三角形 $ ABC $ 一边 $ AB $ 为半径的四分之一圆周，$ P $ 为弧 $ AD $ 上任意一点.若 $ AC = 5 $，则四边形 $ ACBP $ 周长的最大值是(B).


A.$ 15 $
B.$ 15 + 5\sqrt{2} $
C.$ 20 $
D.$ 15 + 5\sqrt{5} $

答案： B

8. 如图 $ 24.1.1 - 4 $，$ M $，$ N $ 为线段 $ AB $ 上的两个三等分点，点 $ A $，$ B $ 在 $\odot O$ 上，求证：$ \angle OMN = \angle ONM $.

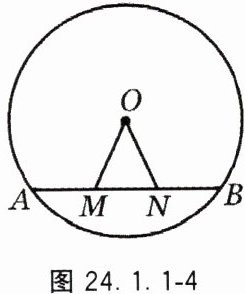
答案： 证明：连接OA，OB。
∵A，B在⊙O上，
∴OA=OB。
∴△OAB是等腰三角形，∠OAB=∠OBA。
∵M，N为AB的三等分点，
∴AM=MN=NB。
在△OAM和△OBN中，
OA=OB，
∠OAM=∠OBN，
AM=BN，
∴△OAM≌△OBN(SAS)。
∴OM=ON。
∴△OMN是等腰三角形。
∴∠OMN=∠ONM。

7. Pai（$\pi$）是什么？数学家说：“$\pi$ 是圆周长与\_\_\_\_\_\_的比.”工程师说：“$\pi$ 大约是 $\dfrac{22}{7}$.”营养学家说：“派是一种好吃的甜点.”

答案： 直径