第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 如图 22.3.2 - 1 所示的是一款抛物线型落地灯示意图,防滑螺母 $ C $ 为抛物线支架的最高点,灯罩 $ D $ 距离地面 $ 1.5 \, m $,最高点 $ C $ 距灯柱的水平距离为 $ 1.6 \, m $,灯柱 $ AB = 1.5 \, m $. 若茶几摆放在灯罩的正下方,则茶几到灯柱的距离 $ AE $ 为(

A.$ 3.2 \, m $
B.$ 0.32 \, m $
C.$ 2.5 \, m $
D.$ 1.6 \, m $
A
).
A.$ 3.2 \, m $
B.$ 0.32 \, m $
C.$ 2.5 \, m $
D.$ 1.6 \, m $
答案:
1. A
2. 小明看到一处喷水景观,喷出的水柱呈抛物线形状,他对此展开研究:测得喷水头 $ P $ 距地面 $ 0.7 \, m $,水柱在距喷水头 $ P $ 水平距离 $ 5 \, m $ 处达到最高,最高点距地面 $ 3.2 \, m $;建立如图 22.3.2 - 2 所示的平面直角坐标系,并设抛物线的表达式为 $ y = a(x - h)^2 + k $,其中 $ x $($ m $)是水柱距喷水头的水平距离,$ y $($ m $)是水柱距地面的高度.
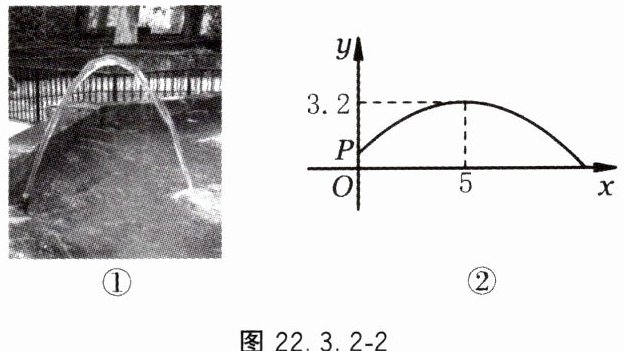
(1) 求抛物线的表达式;
(2) 小明爸爸站在水柱正下方,且距喷水头 $ P $ 水平距离 $ 3 \, m $ 处,身高 $ 1.6 \, m $ 的小明在水柱下方走动,当他的头顶恰好接触到水柱时,求他与爸爸的水平距离.

(1) 求抛物线的表达式;
(2) 小明爸爸站在水柱正下方,且距喷水头 $ P $ 水平距离 $ 3 \, m $ 处,身高 $ 1.6 \, m $ 的小明在水柱下方走动,当他的头顶恰好接触到水柱时,求他与爸爸的水平距离.
答案:
2.(1)$y=-0.1(x-5)^2+3.2$ (2)2 m 或 6 m
3. 掷实心球是某市高中阶段学校招生体育考试的选考项目,一女生投掷过程中,实心球行进路线是一条抛物线,行进高度 $ y $($ m $)与水平距离 $ x $($ m $)之间的函数关系如图 22.3.2 - 3 所示,抛出时起点处高度为 $ \dfrac{5}{3} \, m $,当水平距离为 $ 3 \, m $ 时,实心球行进至最高点 $ 3 \, m $ 处.
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 根据该市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于 $ 6.70 \, m $,此项考试得分为满分 $ 10 $ 分. 问:该女生在此项考试中能否得满分?请说明理由.
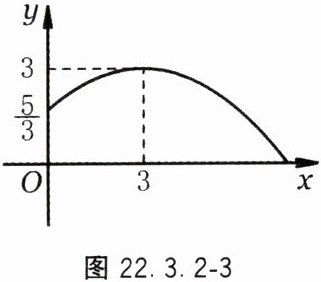
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 根据该市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于 $ 6.70 \, m $,此项考试得分为满分 $ 10 $ 分. 问:该女生在此项考试中能否得满分?请说明理由.

答案:
3.(1)$y=-\dfrac{4}{27}x^2+\dfrac{8}{9}x+\dfrac{5}{3}$ (2)能,理由略
查看更多完整答案,请扫码查看


