第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
9. 如图 22.3.1 - 3,某校九年级学生在数学社团课上进行纸盒设计,利用一个边长为 $ 30 $ cm 的正方形硬纸板,在正方形纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖纸盒。
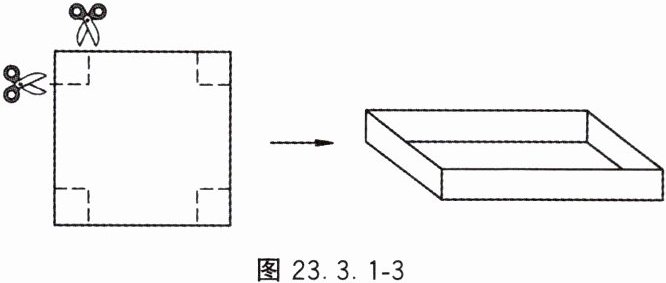
(1) 若无盖纸盒的底面积为 $ 484 $ cm²,则剪掉的小正方形的边长为多少?
(2) 问:折成的无盖纸盒的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,请说明理由。
[img]

(1) 若无盖纸盒的底面积为 $ 484 $ cm²,则剪掉的小正方形的边长为多少?
(2) 问:折成的无盖纸盒的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,请说明理由。
[img]
答案:
(1)4 cm (2)无盖纸盒的侧面积有最大值,当剪掉的小正方形的边长为$\dfrac{15}{2}\ cm$时,最大值为450 cm²
10. 某工厂生产并销售 $ A $, $ B $ 两种型号车床共 $ 14 $ 台,生产并销售 $ 1 $ 台 $ A $ 型车床可以获利 $ 10 $ 万元。若生产并销售不超过 $ 4 $ 台 $ B $ 型车床,则每台 $ B $ 型车床可以获利 $ 17 $ 万元;若超出 $ 4 $ 台 $ B $ 型车床,则每超出 $ 1 $ 台,每台 $ B $ 型车床获利将平均减少 $ 1 $ 万元。设生产并销售 $ B $ 型车床 $ x $ 台。
(1) 当 $ x > 4 $ 时,完成以下两个问题:
① 请补全下面的表格:
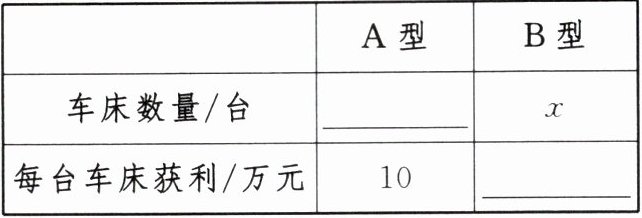
② 若生产并销售 $ B $ 型车床比生产并销售 $ A $ 型车床获得的利润多 $ 70 $ 万元,问:生产并销售 $ B $ 型车床多少台?
(2) 当 $ 0 < x \leq 14 $ 时,设生产并销售 $ A $, $ B $ 两种型号车床获得的总利润为 $ W $ 万元,问:如何分配生产并销售 $ A $, $ B $ 两种车床的数量,可使获得的总利润 $ W $ 最大?最大总利润是多少?
(1) 当 $ x > 4 $ 时,完成以下两个问题:
① 请补全下面的表格:

② 若生产并销售 $ B $ 型车床比生产并销售 $ A $ 型车床获得的利润多 $ 70 $ 万元,问:生产并销售 $ B $ 型车床多少台?
(2) 当 $ 0 < x \leq 14 $ 时,设生产并销售 $ A $, $ B $ 两种型号车床获得的总利润为 $ W $ 万元,问:如何分配生产并销售 $ A $, $ B $ 两种车床的数量,可使获得的总利润 $ W $ 最大?最大总利润是多少?
答案:
(1)①$14-x$ $21-x$ ②10台 (2)产销A型9台、B型5台,或A型8台、B型6台,可获最大总利润170万元
查看更多完整答案,请扫码查看


