《2025年顶尖课课练九年级数学上册人教版》

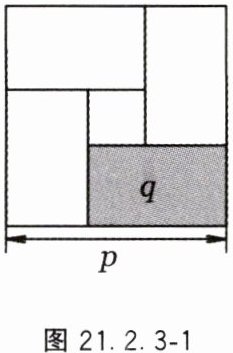
7. 已知长方形的长宽之和为 $p$，面积为 $q$，设宽为 $x$，根据图形面积的关系可构造方程 $x(p - x)=q$。早在公元 $3$ 世纪，我国汉代的赵爽借助图(由四个这样的长方形围成一个大正方形，中空的部分是一个小正方形)将 $x$ 用 $p$，$q$ 表示为 $x=\frac{1}{2}(p-\sqrt{p^{2}-4q})$，从而得到形如 $-x^{2}+px = q$ 的一元二次方程其中一个根的求根公式。结合图 21.2.3 - 1，$x$ 的表达式中 $\sqrt{p^{2}-4q}$ 所表示的几何量是小正方形的边长。

答案： 小正方形的边长

8. 若 $(x + y)(x + y + 2)-8 = 0$，则 $x + y=$2 或$-4$。

答案： 2 或$-4$

9. 阅读题：
解方程：$x^{2}-4|x|-12 = 0$。
解：
当 $x\geq0$ 时，原方程可化为 $x^{2}-4x - 12 = 0$，配方得 $(x - 2)^{2}=16$，$x - 2=\pm4$，$\therefore x_{1}=6$，$x_{2}=-2$（舍去）。
当 $x\lt0$ 时，原方程可化为 $x^{2}+4x - 12 = 0$，配方得 $(x + 2)^{2}=16$，$x + 2=\pm4$，$\therefore x_{3}=-6$，$x_{4}=2$（舍去）。
$\therefore$ 原方程的解为 $x = 6$ 或 $x = -6$。
依上例解方程：$x^{2}-2|x - 1|-4 = 0$。

答案： $x_{1}=1+\sqrt{3}$，$x_{2}=-1-\sqrt{7}$

10. 在一次数学课外活动中，小明给全班同学演示了一个有趣的变形，即在 $\left(\frac{x^{2}-1}{x}\right)^{2}-2\left(\frac{x^{2}-1}{x}\right)+1 = 0$ 中，令 $\frac{x^{2}-1}{x}=y$，则有 $y^{2}-2y + 1 = 0$。根据上述变形的数学思想（换元法）求方程 $(x^{2}-1)^{2}+(x^{2}-1)=0$ 的根。

答案： $x_{1}=1$，$x_{2}=-1$，$x_{3}=x_{4}=0$