《2025年高分突破课时达标讲练测七年级数学上册北师大版》

1. 等式
含有等号的式子叫作等式。表示形式是把两个数或式子用“=”连接起来。

答案： 等号

2. 等式的基本性质
(1)基本性质1:等式的两边都加(或减)同一个代数式,所得结果仍是等式。用字母表示:若$a = b$,则$a \pm c = $$ b \pm c $。
(2)基本性质2:等式的两边都乘同一个数(或除以同一个不为0的数),所得结果仍是等式。用字母表示:若$a = b$,则$ac = $$ bc $;$\frac{a}{m} = $$ \frac{b}{m} $$(m \neq 0)$。
注意:等式的基本性质2中,除以的同一个数一定是非零数。
(3)等式具有对称性和传递性:若$a = b$,则$ b = a $;若$a = b$,$b = c$,则$ a = c $。

答案：
(1)加 减 $ b \pm c $；
(2)乘 除以 0 $ bc $ $ \frac{b}{m} $；
(3)$ b = a $ $ a = c $

(1)根据等式的性质判断,下列变形正确的是 (B)
A.由$-\frac{1}{3}x = \frac{2}{3}y得x = 2y$
B.由$3x - 2 = 2x + 2得x = 4$
C.由$2x - 3 = 3x得x = 3$
D.由$ax = 5a得x = 5$

答案：
(1) B；
 

(2)下列变形:①若$x = y$,则$x + 5 = y - 5$;②若$a = b$,则$ac = bc$;③若$ac = bc$,则$a = b$;④若$a = b$,则$\frac{a}{c^{2} + 1} = \frac{b}{c^{2} + 1}$。其中正确的有______。(填序号)
[易错点拨] 利用等式的基本性质1变形时,要注意符号的变化及同一个数(或代数式)。利用等式的基本性质2变形时,要注意等式两边同时除以的同一个数一定要非零!

答案：
(2)②④

1. 根据等式的性质,下列变形正确的是 (C)
A.若$x = y$,则$x + c = y - c$
B.若$ab = bc$,则$a = c$
C.若$\frac{a}{c} = \frac{b}{c}$,则$a = b$
D.若$\frac{x}{2} + \frac{x}{3} = 1$,则$3x + 2x = 1$

答案： C

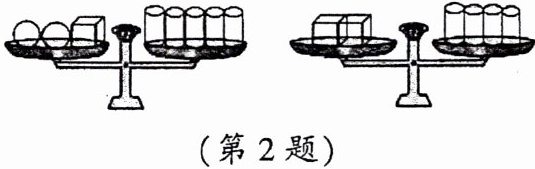
2. (2025·成都期末)如图,两台天平都保持平衡,则与2个球体质量相等的圆柱体的个数为______3。

答案： 3

例2 解下列方程:
(1)$2x - 4 = 0$;
(2)$\frac{1}{3}x + 15 = 8$;
(3)$2y + 3 = 11 - 6y$。
[知识点拨] 利用等式的基本性质解方程,实质就是将方程一步步转化为$x = a$的形式。

答案： $(1)$ 解方程$2x - 4 = 0$
解：
根据等式的基本性质$1$：等式两边同时加上（或减去）同一个整式，等式仍然成立。
在方程$2x - 4 = 0$两边同时加$4$，得到$2x-4 + 4=0 + 4$，即$2x=4$。
再根据等式的基本性质$2$：等式两边同时乘（或除）相等的非零的数或式子，两边依然相等。
在方程$2x = 4$两边同时除以$2$，即$2x÷2 = 4÷2$，解得$x = 2$。
$(2)$ 解方程$\frac{1}{3}x + 15 = 8$
解：
根据等式的基本性质$1$，在方程$\frac{1}{3}x + 15 = 8$两边同时减$15$，得到$\frac{1}{3}x+15 - 15=8 - 15$，即$\frac{1}{3}x=-7$。
再根据等式的基本性质$2$，在方程$\frac{1}{3}x=-7$两边同时乘$3$，即$\frac{1}{3}x×3=-7×3$，解得$x=-21$。
$(3)$ 解方程$2y + 3 = 11 - 6y$
解：
根据等式的基本性质$1$，在方程$2y + 3 = 11 - 6y$两边同时加$6y$，得到$2y+3 + 6y=11 - 6y+6y$，即$8y + 3 = 11$。
然后在方程$8y + 3 = 11$两边同时减$3$，得到$8y+3 - 3=11 - 3$，即$8y = 8$。
最后根据等式的基本性质$2$，在方程$8y = 8$两边同时除以$8$，即$8y÷8 = 8÷8$，解得$y = 1$。
综上，$(1)$ $x = 2$；$(2)$ $x=-21$；$(3)$ $y = 1$。