第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
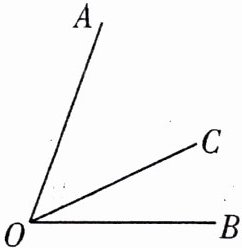
例3 (1) 如图,射线$OC在∠AOB$的内部,尺规作图:在$∠AOB的外部作∠AOD$,使$∠AOD = ∠BOC$;(要求:不写作法,保留作图痕迹)
(2) 如图,已知$∠α和∠β$,$∠α < ∠β$。用直尺和圆规作两个角,使其大小分别为$∠β - ∠α$。
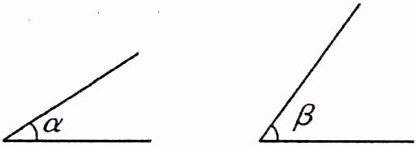

(2) 如图,已知$∠α和∠β$,$∠α < ∠β$。用直尺和圆规作两个角,使其大小分别为$∠β - ∠α$。
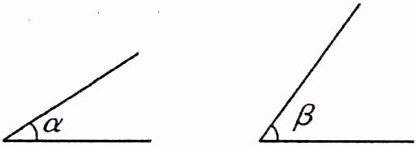
答案:
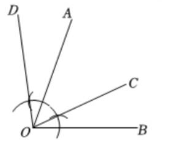


6. 如图,点$C在∠AOB的OB$边上,用尺规作出了$∠NCE = ∠AOD$,作图痕迹中,弧$FG$是(
A.以点$C$为圆心,$OD$为半径的弧
B.以点$C$为圆心,$DM$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DM$为半径的弧
D
)A.以点$C$为圆心,$OD$为半径的弧
B.以点$C$为圆心,$DM$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DM$为半径的弧
答案:
6.D
1. 多边形的相关概念
(1)定义:由若干条不在同一直线上的线段
(2)多边形的对角线:在多边形中,连接
(3)正多边形:
(1)定义:由若干条不在同一直线上的线段
首尾顺次
相连组成的封闭平面图形叫作多边形。根据多边形的边数的多少,可以将多边形分成三角形、四边形、五边形等。(2)多边形的对角线:在多边形中,连接
不相邻
两个顶点的线段叫作多边形的对角线。注:过n边形的每一个顶点有n-3条对角线,n边形共有$\frac {n(n-3)}{2}$条对角线。(3)正多边形:
各边
相等,各角
也相等的多边形叫作正多边形。
答案:
(1)首尾顺次
(2)不相邻
(3)各边 各角
(1)首尾顺次
(2)不相邻
(3)各边 各角
2. 圆的相关概念
(1)定义:平面上,一条线段绕着它固定的一个端点旋转
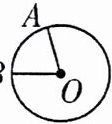
(2)弧:圆上任意两点A,B间的部分叫作圆弧,简称
(3)扇形:由一条弧和经过这条弧的端点的两条半径所组成的图形叫作扇形。
(4)圆心角:顶点在
(5)半圆是特殊的弧,半圆形是特殊的扇形。
(1)定义:平面上,一条线段绕着它固定的一个端点旋转
一周
,另一个端点形成的图形叫作圆。固定的端点称为圆心
,这条线段称为半径。如图中O为圆心,OA,OB为半径。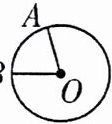
(2)弧:圆上任意两点A,B间的部分叫作圆弧,简称
弧
,记作$\overset{\frown }{AB}$,读作“圆弧AB”或“弧AB”。(3)扇形:由一条弧和经过这条弧的端点的两条半径所组成的图形叫作扇形。
(4)圆心角:顶点在
圆心
的角叫作圆心角。若点O为圆心,点A,B在圆上,则∠AOB就是一个圆心角。(5)半圆是特殊的弧,半圆形是特殊的扇形。
答案:
(1)一周 圆心
(2)弧
(4)圆心
(1)一周 圆心
(2)弧
(4)圆心
(1)用字母表示图中五边形的边、顶点、内角;
边:
(2)从八边形的一个顶点可以引
(3)从多边形的一个顶点可以引出3条对角线,则这个多边形是
边:
AB,BC,CD,DE,EA
;顶点:A,B,C,D,E
;内角:∠A,∠B,∠C,∠D,∠E
(2)从八边形的一个顶点可以引
5
条对角线,将八边形分割为6
个三角形,八边形总共有20
条对角线;(3)从多边形的一个顶点可以引出3条对角线,则这个多边形是
六边形
。
答案:
(1)AB BC CD DE EA A B C D E ∠A ∠B ∠C ∠D ∠E
(2)5 6 20
(3)六边形
(1)AB BC CD DE EA A B C D E ∠A ∠B ∠C ∠D ∠E
(2)5 6 20
(3)六边形
查看更多完整答案,请扫码查看


