第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例2 (1) 如图1,已知$AB与CD相交于点O$,且$∠DOE = ∠AOC$,$OF平分∠AOE$,若$∠AOC = 28^{\circ}$,求$∠EOF$的度数;
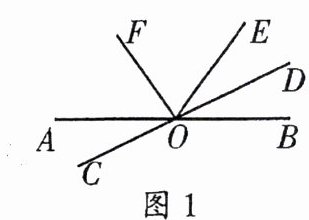
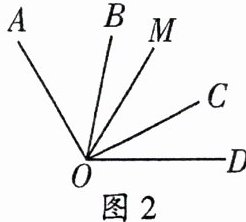
(2) 如图2,$∠AOB : ∠BOC : ∠COD = 4 : 5 : 3$,$OM平分∠AOD$,$∠BOM = 20^{\circ}$,求$∠AOD和∠MOC$的度数。


(2) 如图2,$∠AOB : ∠BOC : ∠COD = 4 : 5 : 3$,$OM平分∠AOD$,$∠BOM = 20^{\circ}$,求$∠AOD和∠MOC$的度数。
答案:
$(1)$求$\angle EOF$的度数
解:
- 因为$AB$与$CD$相交于点$O$,所以$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,可得$\angle BOD=\angle AOC = 28^{\circ}$。
- 又因为$\angle DOE=\angle AOC = 28^{\circ}$,且$\angle AOE+\angle DOE+\angle BOD = 180^{\circ}$(平角为$180^{\circ}$),所以$\angle AOE=180^{\circ}-\angle DOE - \angle BOD=180^{\circ}-28^{\circ}-28^{\circ}=124^{\circ}$。
- 由于$OF$平分$\angle AOE$,根据角平分线定义,$\angle EOF=\frac{1}{2}\angle AOE$,即$\angle EOF=\frac{1}{2}×124^{\circ}=62^{\circ}$。
$(2)$求$\angle AOD$和$\angle MOC$的度数
解:
- 设$\angle AOB = 4x$,$\angle BOC = 5x$,$\angle COD = 3x$,则$\angle AOD=\angle AOB+\angle BOC+\angle COD=4x + 5x+3x = 12x$。
- 因为$OM$平分$\angle AOD$,所以$\angle AOM=\frac{1}{2}\angle AOD = 6x$。
- 又因为$\angle AOM=\angle AOB+\angle BOM$,已知$\angle BOM = 20^{\circ}$,所以$6x=4x + 20^{\circ}$。
移项可得:$6x-4x=20^{\circ}$,即$2x = 20^{\circ}$,解得$x = 10^{\circ}$。
- 那么$\angle AOD=12x=12×10^{\circ}=120^{\circ}$。
- $\angle MOC=\angle BOC-\angle BOM$,$\angle BOC = 5x = 5×10^{\circ}=50^{\circ}$,所以$\angle MOC=50^{\circ}-20^{\circ}=30^{\circ}$。
综上,$(1)$$\boldsymbol{\angle EOF = 62^{\circ}}$;$(2)$$\boldsymbol{\angle AOD = 120^{\circ}}$,$\boldsymbol{\angle MOC = 30^{\circ}}$。
解:
- 因为$AB$与$CD$相交于点$O$,所以$\angle AOC$与$\angle BOD$是对顶角,根据对顶角相等,可得$\angle BOD=\angle AOC = 28^{\circ}$。
- 又因为$\angle DOE=\angle AOC = 28^{\circ}$,且$\angle AOE+\angle DOE+\angle BOD = 180^{\circ}$(平角为$180^{\circ}$),所以$\angle AOE=180^{\circ}-\angle DOE - \angle BOD=180^{\circ}-28^{\circ}-28^{\circ}=124^{\circ}$。
- 由于$OF$平分$\angle AOE$,根据角平分线定义,$\angle EOF=\frac{1}{2}\angle AOE$,即$\angle EOF=\frac{1}{2}×124^{\circ}=62^{\circ}$。
$(2)$求$\angle AOD$和$\angle MOC$的度数
解:
- 设$\angle AOB = 4x$,$\angle BOC = 5x$,$\angle COD = 3x$,则$\angle AOD=\angle AOB+\angle BOC+\angle COD=4x + 5x+3x = 12x$。
- 因为$OM$平分$\angle AOD$,所以$\angle AOM=\frac{1}{2}\angle AOD = 6x$。
- 又因为$\angle AOM=\angle AOB+\angle BOM$,已知$\angle BOM = 20^{\circ}$,所以$6x=4x + 20^{\circ}$。
移项可得:$6x-4x=20^{\circ}$,即$2x = 20^{\circ}$,解得$x = 10^{\circ}$。
- 那么$\angle AOD=12x=12×10^{\circ}=120^{\circ}$。
- $\angle MOC=\angle BOC-\angle BOM$,$\angle BOC = 5x = 5×10^{\circ}=50^{\circ}$,所以$\angle MOC=50^{\circ}-20^{\circ}=30^{\circ}$。
综上,$(1)$$\boldsymbol{\angle EOF = 62^{\circ}}$;$(2)$$\boldsymbol{\angle AOD = 120^{\circ}}$,$\boldsymbol{\angle MOC = 30^{\circ}}$。
3. 如图,点$O为直线AB$上一点,$OE平分∠AOD$,$∠EOC = ∠BOD$,$∠DOC = 60^{\circ}$,则$∠AOE$的度数为(
A.$34^{\circ}$
B.$36^{\circ}$
C.$38^{\circ}$
D.$40^{\circ}$
D
)A.$34^{\circ}$
B.$36^{\circ}$
C.$38^{\circ}$
D.$40^{\circ}$
答案:
3.D;
4. 已知$∠AOB = 60^{\circ}$,$OC平分∠AOB$,以$OC为一边作∠COP = 15^{\circ}$,则$∠BOP$的度数为______。
答案:
4.15°或45°
5. (2025·重庆巴南区)如图,已知$∠AOC = 120^{\circ}$,$OE是∠BOC$的平分线,且$∠DOE = 80^{\circ}$。
(1) 求$∠COE和∠COD$的度数;
(2) 在$∠AOD内作射线OF$,使得$∠DOF : ∠AOF = 3 : 4$,求$∠EOF$的度数。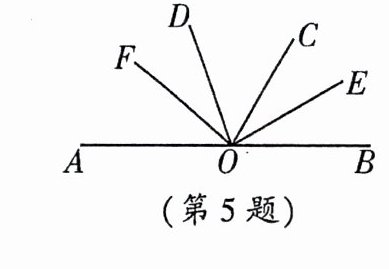
(1) 求$∠COE和∠COD$的度数;
(2) 在$∠AOD内作射线OF$,使得$∠DOF : ∠AOF = 3 : 4$,求$∠EOF$的度数。

答案:
5.
(1)∠COE=30°, ∠COD=50°;
(2)∠EOF=110°
(1)∠COE=30°, ∠COD=50°;
(2)∠EOF=110°
查看更多完整答案,请扫码查看


