第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例1 如图,设A,B,C,D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问应把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?请说明理由。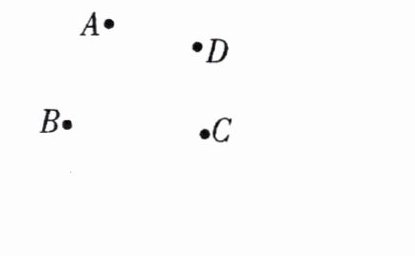
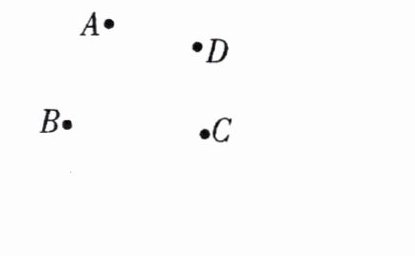
答案:
解:应建在对角线$AC$与$BD$的交点处。
理由:设对角线$AC$与$BD$交点为$O$,另取一点$O'$。
根据三角形两边之和大于第三边,在$\triangle AO'D$中,$AO' + DO' > AD$($AD = AO + DO$);在$\triangle BO'C$中,$BO' + CO' > BC$($BC = BO + CO$)。
则$AO' + BO' + CO' + DO' > AO + BO + CO + DO$,即对角线交点$O$到$A$、$B$、$C$、$D$四个居民小区的距离之和最小。
理由:设对角线$AC$与$BD$交点为$O$,另取一点$O'$。
根据三角形两边之和大于第三边,在$\triangle AO'D$中,$AO' + DO' > AD$($AD = AO + DO$);在$\triangle BO'C$中,$BO' + CO' > BC$($BC = BO + CO$)。
则$AO' + BO' + CO' + DO' > AO + BO + CO + DO$,即对角线交点$O$到$A$、$B$、$C$、$D$四个居民小区的距离之和最小。
1. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是 (
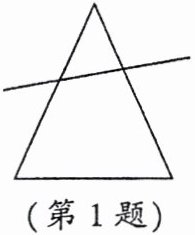
A.四边形周长小于三角形周长
B.两点确定一条直线
C.两点之间,线段最短
D.经过一点有无数条直线
C
)
A.四边形周长小于三角形周长
B.两点确定一条直线
C.两点之间,线段最短
D.经过一点有无数条直线
答案:
C
①AB + BC =
②AB = AD -
③AB + CD = AD -
④AC + BD = AD +
AC
;②AB = AD -
BD
= AC - BC
;③AB + CD = AD -
BC
;④AC + BD = AD +
BC
。
答案:
①AC ②BD BC ③BC ④BC
2. 如图,AB = CD,那么AC与BD的大小关系是 (
A.AC = BD
B.AC < BD
C.AC > BD
D.不能确定
A
)A.AC = BD
B.AC < BD
C.AC > BD
D.不能确定
答案:
2.A
3. 下列条件中,点A,B,C不可能在同一条直线上的是 ( )
A.AB = 4cm,BC = 6cm,AC = 2cm
B.AB = 8cm,BC = 5cm,AC = 4cm
C.AB = 17cm,BC = 7cm,AC = 10cm
D.AB = 3cm,BC = 9cm,AC = 6cm
A.AB = 4cm,BC = 6cm,AC = 2cm
B.AB = 8cm,BC = 5cm,AC = 4cm
C.AB = 17cm,BC = 7cm,AC = 10cm
D.AB = 3cm,BC = 9cm,AC = 6cm
答案:
B
4. 看图填空:
(1) AC = ____ + AB;
(2) AD - AB = ____ = AC - ____ + CD。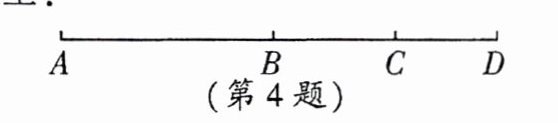
(1) AC = ____ + AB;
(2) AD - AB = ____ = AC - ____ + CD。

答案:
4.
(1)BC
(2)BD AB
(1)BC
(2)BD AB
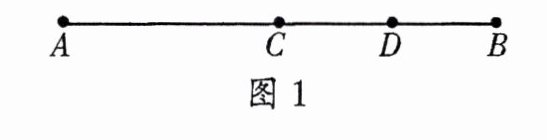
例3 (1) 如图1,AB = 6cm,点C是线段AB的中点,点D是线段BC的中点,求线段AD的长;

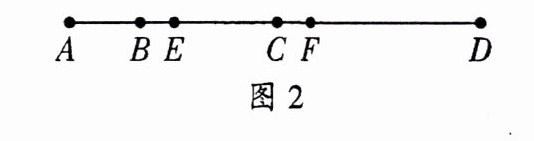
(2) (2025·重庆育才)如图2,点A,B,C,D在同一直线上,已知AB = $\frac{1}{3}AC$,BC = $\frac{2}{3}CD$,且点E,F分别是AC,BD的中点。若EF = 8,求AF的长;
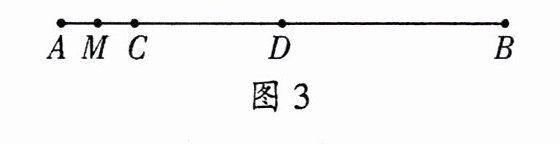
(3) 如图3,已知线段AB上有两点C,D,使得AC:CD:DB = 1:2:3,点M是线段AC的中点,点N是线段AB上的点,且满足DN = $\frac{1}{4}DB$,AB = 24。求线段MN的长。
[思维点拨] 运用线段中点的性质进行计算或推理时,注意结合图形进行分析(数形结合),常常会因点的位置不确定而进行分类讨论。


(2) (2025·重庆育才)如图2,点A,B,C,D在同一直线上,已知AB = $\frac{1}{3}AC$,BC = $\frac{2}{3}CD$,且点E,F分别是AC,BD的中点。若EF = 8,求AF的长;

(3) 如图3,已知线段AB上有两点C,D,使得AC:CD:DB = 1:2:3,点M是线段AC的中点,点N是线段AB上的点,且满足DN = $\frac{1}{4}DB$,AB = 24。求线段MN的长。

[思维点拨] 运用线段中点的性质进行计算或推理时,注意结合图形进行分析(数形结合),常常会因点的位置不确定而进行分类讨论。
答案:
$(1)$ 求线段$AD$的长
解:
因为点$C$是线段$AB$的中点,$AB = 6cm$,根据线段中点的定义:若点$C$是线段$AB$中点,则$AC=BC=\frac{1}{2}AB$,所以$AC = BC=\frac{1}{2}×6 = 3cm$。
又因为点$D$是线段$BC$的中点,所以$CD=\frac{1}{2}BC$,则$CD=\frac{1}{2}×3 = 1.5cm$。
根据线段的和的关系$AD=AC + CD$,可得$AD=3 + 1.5=4.5cm$。
$(2)$ 求$AF$的长
解:
设$AB=x$,因为$AB=\frac{1}{3}AC$,所以$AC = 3x$,则$BC=AC - AB=3x - x = 2x$。
又因为$BC=\frac{2}{3}CD$,所以$CD = 3x$,$BD=BC + CD=2x+3x = 5x$。
因为点$E$是$AC$的中点,所以$AE=EC=\frac{1}{2}AC=\frac{3}{2}x$;因为点$F$是$BD$的中点,所以$BF=FD=\frac{1}{2}BD=\frac{5}{2}x$。
$EF=EC+CF$,$CF=BF - BC$,即$CF=\frac{5}{2}x-2x=\frac{1}{2}x$,$EF=\frac{3}{2}x+\frac{1}{2}x = 2x$。
已知$EF = 8$,即$2x = 8$,解得$x = 4$。
$AF=AB+BF$,$BF=\frac{5}{2}x$,$x = 4$,所以$BF=\frac{5}{2}×4 = 10$,$AB = 4$,则$AF=4 + 10=14$。
$(3)$ 求线段$MN$的长
解:
因为$AC:CD:DB = 1:2:3$,设$AC=x$,$CD = 2x$,$DB = 3x$,则$AB=AC + CD+DB=x + 2x+3x=6x$。
已知$AB = 24$,即$6x = 24$,解得$x = 4$。
所以$AC = 4$,$CD = 8$,$DB = 12$。
因为点$M$是线段$AC$的中点,所以$AM=MC=\frac{1}{2}AC=\frac{1}{2}×4 = 2$。
因为$DN=\frac{1}{4}DB$,所以$DN=\frac{1}{4}×12 = 3$。
分两种情况讨论:
当点$N$在线段$DB$上时,$MN=MC+CD+DN=2 + 8+3=13$。
当点$N$在线段$AD$上时,$MN=MC+CD - DN=2 + 8-3=7$。
综上,$(1)$$\boldsymbol{4.5cm}$;$(2)$$\boldsymbol{14}$;$(3)$$\boldsymbol{7}$或$\boldsymbol{13}$。
解:
因为点$C$是线段$AB$的中点,$AB = 6cm$,根据线段中点的定义:若点$C$是线段$AB$中点,则$AC=BC=\frac{1}{2}AB$,所以$AC = BC=\frac{1}{2}×6 = 3cm$。
又因为点$D$是线段$BC$的中点,所以$CD=\frac{1}{2}BC$,则$CD=\frac{1}{2}×3 = 1.5cm$。
根据线段的和的关系$AD=AC + CD$,可得$AD=3 + 1.5=4.5cm$。
$(2)$ 求$AF$的长
解:
设$AB=x$,因为$AB=\frac{1}{3}AC$,所以$AC = 3x$,则$BC=AC - AB=3x - x = 2x$。
又因为$BC=\frac{2}{3}CD$,所以$CD = 3x$,$BD=BC + CD=2x+3x = 5x$。
因为点$E$是$AC$的中点,所以$AE=EC=\frac{1}{2}AC=\frac{3}{2}x$;因为点$F$是$BD$的中点,所以$BF=FD=\frac{1}{2}BD=\frac{5}{2}x$。
$EF=EC+CF$,$CF=BF - BC$,即$CF=\frac{5}{2}x-2x=\frac{1}{2}x$,$EF=\frac{3}{2}x+\frac{1}{2}x = 2x$。
已知$EF = 8$,即$2x = 8$,解得$x = 4$。
$AF=AB+BF$,$BF=\frac{5}{2}x$,$x = 4$,所以$BF=\frac{5}{2}×4 = 10$,$AB = 4$,则$AF=4 + 10=14$。
$(3)$ 求线段$MN$的长
解:
因为$AC:CD:DB = 1:2:3$,设$AC=x$,$CD = 2x$,$DB = 3x$,则$AB=AC + CD+DB=x + 2x+3x=6x$。
已知$AB = 24$,即$6x = 24$,解得$x = 4$。
所以$AC = 4$,$CD = 8$,$DB = 12$。
因为点$M$是线段$AC$的中点,所以$AM=MC=\frac{1}{2}AC=\frac{1}{2}×4 = 2$。
因为$DN=\frac{1}{4}DB$,所以$DN=\frac{1}{4}×12 = 3$。
分两种情况讨论:
当点$N$在线段$DB$上时,$MN=MC+CD+DN=2 + 8+3=13$。
当点$N$在线段$AD$上时,$MN=MC+CD - DN=2 + 8-3=7$。
综上,$(1)$$\boldsymbol{4.5cm}$;$(2)$$\boldsymbol{14}$;$(3)$$\boldsymbol{7}$或$\boldsymbol{13}$。
查看更多完整答案,请扫码查看


