第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例2 (1) 经过平面内的三点可以画几条直线?
(2) 平面内5个点最多可以画多少条直线?
(3) 平面内有n(n≥2)个点最多可以画多少条直线呢?
[分析] ① 平面内的三点的位置有两种可能:三点在同一条直线上(如图1);三点不在同一条直线上(如图2)。② 当任意三点不在一条直线上时,得到直线条数最多。
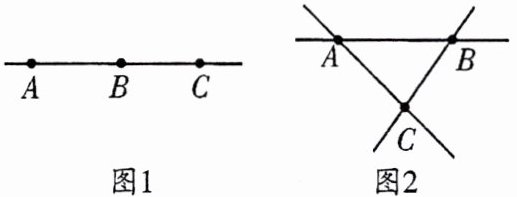
[结论总结] (1) 若一条直线上共有n个点,则直线上共有$\frac{n(n - 1)}{2}$条线段,2n条射线。(2) 若平面内有n个点(无三点共线的情况),则能画$\frac{n(n - 1)}{2}$条直线。(3) 在同一平面内,n条直线相交,最多有$\frac{n(n - 1)}{2}$个交点。
(2) 平面内5个点最多可以画多少条直线?
(3) 平面内有n(n≥2)个点最多可以画多少条直线呢?
[分析] ① 平面内的三点的位置有两种可能:三点在同一条直线上(如图1);三点不在同一条直线上(如图2)。② 当任意三点不在一条直线上时,得到直线条数最多。
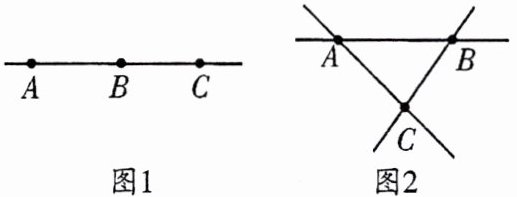
[结论总结] (1) 若一条直线上共有n个点,则直线上共有$\frac{n(n - 1)}{2}$条线段,2n条射线。(2) 若平面内有n个点(无三点共线的情况),则能画$\frac{n(n - 1)}{2}$条直线。(3) 在同一平面内,n条直线相交,最多有$\frac{n(n - 1)}{2}$个交点。
答案:
(1)1条或3条
(2)10条
(3)$\frac{n(n-1)}{2}$条
(1)1条或3条
(2)10条
(3)$\frac{n(n-1)}{2}$条
3. 如图,图中有x条直线,y条线段,z条射线,则3x + y + z =
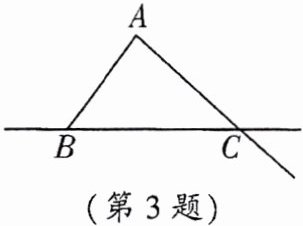
12
。
答案:
3.12
4. 往返于A,B两地的火车,中途停靠三个站(各站之间距离不等),则有____种不同的票价,要准备____种不同的车票。
答案:
4.10 20
1. 线段的性质
两点之间的所有连线中,
两点之间的所有连线中,
线段
最短,简记为两点之间线段最短
。
答案:
线段 两点之间线段最短
2. 两点之间的距离
两点之间
注意:距离是指线段的长度,是一个数值,而不是线段本身。因此,不能说“A,B两点间的距离是线段AB”,而应该是“A,B两点间的距离是线段AB的长度”。
两点之间
线段的长度
,叫作这两点之间的距离。注意:距离是指线段的长度,是一个数值,而不是线段本身。因此,不能说“A,B两点间的距离是线段AB”,而应该是“A,B两点间的距离是线段AB的长度”。
答案:
线段的长度
3. 比较两条线段的长度的方法
(1) 观察法;
(2) 度量法:用刻度尺量出它们的长度,再进行比较;
(3) 叠合法:把其中的一条线段移到另一条线段上去,将其中的一个端点
思考:下面的情境用到了哪些比较线段长短的方法?
小的时候你矮矮个儿,妈妈高高个儿,你们俩谁高?怎么比较出来的? (
慢慢长大以后,你们的身高差距不再明显,怎么比身高呢? (
再以后,你去遥远的地方念书,只能通过电话告诉她:“妈妈,我有165cm了,比你高了5cm。” (
(1) 观察法;
(2) 度量法:用刻度尺量出它们的长度,再进行比较;
(3) 叠合法:把其中的一条线段移到另一条线段上去,将其中的一个端点
重合
在一起加以比较。思考:下面的情境用到了哪些比较线段长短的方法?
小的时候你矮矮个儿,妈妈高高个儿,你们俩谁高?怎么比较出来的? (
看
)慢慢长大以后,你们的身高差距不再明显,怎么比身高呢? (
背靠背
)再以后,你去遥远的地方念书,只能通过电话告诉她:“妈妈,我有165cm了,比你高了5cm。” (
度量法
)
答案:
(3)重合 思考:看 背靠背 度量法
(3)重合 思考:看 背靠背 度量法
4. 尺规作图
(1) 限定用没有刻度的直尺和圆规作图,称为尺规作图。
(2) 作一条线段等于已知线段a的步骤:(如图1)
①作射线AP;
②用圆规在射线AP上截取AB = a。
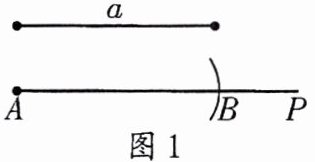
(1) 限定用没有刻度的直尺和圆规作图,称为尺规作图。
(2) 作一条线段等于已知线段a的步骤:(如图1)
①作射线AP;
②用圆规在射线AP上截取AB = a。


答案:
步骤如上所述。
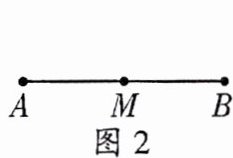
如图2,如果点M把线段AB分成
相等
的两条线段AM与BM,点M叫作线段AB的中点。
答案:
相等
查看更多完整答案,请扫码查看


