第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例 1 用代数式表示:
(1)x 与 y 的差;
(2)a 除以 b 的商与 c 的和;
(3)一个三位数,百位数字为 x,十位数字是 y,个位数字为 z,表示这个三位数;
(4)比 a,b 和的平方的倒数小 5 的数。
(1)x 与 y 的差;
(2)a 除以 b 的商与 c 的和;
(3)一个三位数,百位数字为 x,十位数字是 y,个位数字为 z,表示这个三位数;
(4)比 a,b 和的平方的倒数小 5 的数。
答案:
(1)$x-y$
(2)$\frac {a}{b}+c$
(3)$100x+10y+z$
(4)$\frac {1}{(a+b)^{2}}-5$
(1)$x-y$
(2)$\frac {a}{b}+c$
(3)$100x+10y+z$
(4)$\frac {1}{(a+b)^{2}}-5$
1. 代数式$\frac {x-y}{2}$的意义是 (
A.x 与 y 的一半的差
B.x 减去 y 除以 2 的差
C.x 与 y 的差的一半
D.x 与 y 的$\frac {1}{2}$的差
C
)A.x 与 y 的一半的差
B.x 减去 y 除以 2 的差
C.x 与 y 的差的一半
D.x 与 y 的$\frac {1}{2}$的差
答案:
1.C
2. 在下列各题的横线上填上适当的代数式。
(1)设甲数为 a,乙数比甲数的$1\frac {1}{3}$倍少 3,则乙数为____;
(2)被 4 除,其商为 m,余数是 3 的数用代数式表示为____;
(3)a 的 2 倍与 b 的$\frac {2}{5}$的差的平方,用代数式表示为____。
(1)设甲数为 a,乙数比甲数的$1\frac {1}{3}$倍少 3,则乙数为____;
(2)被 4 除,其商为 m,余数是 3 的数用代数式表示为____;
(3)a 的 2 倍与 b 的$\frac {2}{5}$的差的平方,用代数式表示为____。
答案:
2.
(1)$\frac {4}{3}a-3$
(2)$4m+3$
(3)$(2a-\frac {2}{5}b)^{2}$
(1)$\frac {4}{3}a-3$
(2)$4m+3$
(3)$(2a-\frac {2}{5}b)^{2}$
例 2 (1)当$x= 1,y= -6$时,求下列代数式的值:
①$x^{2}+y^{2}$;
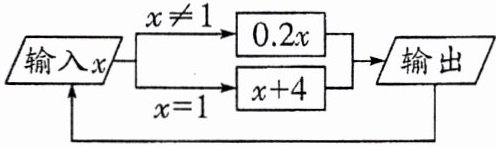
(2)如图是一个运算程序的示意图,若开始输入 x 的值为 3125,则第 2025 次输出的结果为____。
①$x^{2}+y^{2}$;
37
②$(x+y)^{2}$;25
③$x^{2}-2xy+y^{2}$。49
(2)如图是一个运算程序的示意图,若开始输入 x 的值为 3125,则第 2025 次输出的结果为____。
1

答案:
1. (1)
①解:
当$x = 1$,$y=-6$时,根据公式$a^{2}+b^{2}$(这里$a = x$,$b = y$),对于$x^{2}+y^{2}$,将$x = 1$,$y=-6$代入可得:
$x^{2}+y^{2}=1^{2}+(-6)^{2}$。
根据$a^{2}=a× a$,$1^{2}=1×1 = 1$,$(-6)^{2}=(-6)×(-6)=36$。
所以$x^{2}+y^{2}=1 + 36=37$。
②解:
当$x = 1$,$y=-6$时,根据公式$(a + b)^{2}=a^{2}+2ab + b^{2}$(这里$a = x$,$b = y$),对于$(x + y)^{2}$,先计算$x + y$的值:$x + y=1+( - 6)=1-6=-5$。
再根据$(a)^{2}=a× a$,$(x + y)^{2}=(-5)^{2}=(-5)×(-5)=25$。
③解:
当$x = 1$,$y=-6$时,根据公式$a^{2}-2ab + b^{2}=(a - b)^{2}$(这里$a = x$,$b = y$),对于$x^{2}-2xy + y^{2}$,先计算$x-y$的值:$x - y=1-(-6)=1 + 6=7$。
再根据$(a)^{2}=a× a$,$x^{2}-2xy + y^{2}=(x - y)^{2}=7^{2}=7×7 = 49$。
2. (2)
当$x = 3125$时,因为$x\neq1$,所以输出$0.2x$,$0.2×3125 = 625$;
当$x = 625$时,因为$x\neq1$,所以输出$0.2x$,$0.2×625 = 125$;
当$x = 125$时,因为$x\neq1$,所以输出$0.2x$,$0.2×125 = 25$;
当$x = 25$时,因为$x\neq1$,所以输出$0.2x$,$0.2×25 = 5$;
当$x = 5$时,因为$x\neq1$,所以输出$0.2x$,$0.2×5 = 1$;
当$x = 1$时,输出$x + 4=1 + 4=5$;
当$x = 5$时,输出$0.2x = 1$,当$x = 1$时,输出$x + 4 = 5$,$\cdots$,可以发现从第$5$次开始,输出结果以$1$,$5$循环。
因为$(2025 - 4)÷2=(2021)÷2 = 1010\cdots\cdots1$。
所以第$2025$次输出的结果为$1$。
综上,(1)①$37$;②$25$;③$49$;(2)$1$。
①解:
当$x = 1$,$y=-6$时,根据公式$a^{2}+b^{2}$(这里$a = x$,$b = y$),对于$x^{2}+y^{2}$,将$x = 1$,$y=-6$代入可得:
$x^{2}+y^{2}=1^{2}+(-6)^{2}$。
根据$a^{2}=a× a$,$1^{2}=1×1 = 1$,$(-6)^{2}=(-6)×(-6)=36$。
所以$x^{2}+y^{2}=1 + 36=37$。
②解:
当$x = 1$,$y=-6$时,根据公式$(a + b)^{2}=a^{2}+2ab + b^{2}$(这里$a = x$,$b = y$),对于$(x + y)^{2}$,先计算$x + y$的值:$x + y=1+( - 6)=1-6=-5$。
再根据$(a)^{2}=a× a$,$(x + y)^{2}=(-5)^{2}=(-5)×(-5)=25$。
③解:
当$x = 1$,$y=-6$时,根据公式$a^{2}-2ab + b^{2}=(a - b)^{2}$(这里$a = x$,$b = y$),对于$x^{2}-2xy + y^{2}$,先计算$x-y$的值:$x - y=1-(-6)=1 + 6=7$。
再根据$(a)^{2}=a× a$,$x^{2}-2xy + y^{2}=(x - y)^{2}=7^{2}=7×7 = 49$。
2. (2)
当$x = 3125$时,因为$x\neq1$,所以输出$0.2x$,$0.2×3125 = 625$;
当$x = 625$时,因为$x\neq1$,所以输出$0.2x$,$0.2×625 = 125$;
当$x = 125$时,因为$x\neq1$,所以输出$0.2x$,$0.2×125 = 25$;
当$x = 25$时,因为$x\neq1$,所以输出$0.2x$,$0.2×25 = 5$;
当$x = 5$时,因为$x\neq1$,所以输出$0.2x$,$0.2×5 = 1$;
当$x = 1$时,输出$x + 4=1 + 4=5$;
当$x = 5$时,输出$0.2x = 1$,当$x = 1$时,输出$x + 4 = 5$,$\cdots$,可以发现从第$5$次开始,输出结果以$1$,$5$循环。
因为$(2025 - 4)÷2=(2021)÷2 = 1010\cdots\cdots1$。
所以第$2025$次输出的结果为$1$。
综上,(1)①$37$;②$25$;③$49$;(2)$1$。
3. 如图,当输入 x 的值为-1 时,输出的结果为 (
A.-1
B.11
C.21
D.43
B
)A.-1
B.11
C.21
D.43
答案:
3.B
4. 已知 a,b 是有理数,且$ab<0$,若$x= \frac {a}{|a|}+\frac {b}{|b|}+\frac {ab}{|ab|}$,则代数式$x^{2}+2x+1$的值为____。
答案:
4. 因为$ab<0$,所以$a$,$b$异号,不妨设$a>0$,$b<0$,则$\frac{a}{|a|}=1$,$\frac{b}{|b|}=-1$,$\frac{ab}{|ab|}=-1$,$x=1 + (-1)+(-1)=-1$,$x^2 + 2x + 1=(-1)^2+2×(-1)+1=0$;若$a<0$,$b>0$,同理可得$x=-1 + 1+(-1)=-1$,$x^2 + 2x + 1=0$,故答案为$0$。
例 3 (1)如果代数式$x^{2}-2x+5$的值等于 7,则代数式$3x^{2}-6x-1$的值为 (
A. 5
B. 6
C. 7
D. 8
(2)当$\frac {m-n}{m+n}= 3$时,求代数式$\frac {m-n}{m+n}-\frac {2(m+n)}{m-n}$的值。
A
)A. 5
B. 6
C. 7
D. 8
(2)当$\frac {m-n}{m+n}= 3$时,求代数式$\frac {m-n}{m+n}-\frac {2(m+n)}{m-n}$的值。
$2\frac {1}{3}$
答案:
(1)A
(2)$2\frac {1}{3}$
(1)A
(2)$2\frac {1}{3}$
5. 已知$a+b= 4$,则代数式$1+\frac {a}{2}+\frac {b}{2}$的值为 (
A.3
B.1
C.0
D.-1
A
)A.3
B.1
C.0
D.-1
答案:
5.A
6. (1)若$x-3y= 3$,则$5+2x-6y= $____,$y-\frac {1}{3}x+\frac {1}{2}= $____;
(2)若$|a-b+3|+(ab-4)^{2}= 0$,则代数式$3a+2ab-3b$的值为____;
(3)当$x= 2$时,代数式$ax^{3}+bx+1$的值为 6,那么当$x= -2$时,代数式$ax^{3}+bx+1$的值是____。
(2)若$|a-b+3|+(ab-4)^{2}= 0$,则代数式$3a+2ab-3b$的值为____;
(3)当$x= 2$时,代数式$ax^{3}+bx+1$的值为 6,那么当$x= -2$时,代数式$ax^{3}+bx+1$的值是____。
答案:
6.
(1)11 $-\frac {1}{2}$
(2)-1
(3)-4
(1)11 $-\frac {1}{2}$
(2)-1
(3)-4
查看更多完整答案,请扫码查看


