《2025年课时提优计划作业本七年级数学上册苏科版》

1. 下列代数式中,符合代数式书写要求的是(A)
A.$\frac{3m}{n}$
B.$3\frac{1}{5}x^{2}y$
C.$m+n$米
D.$ab\cdot 3$

答案： A

2. 一双运动鞋原价为$a$元,网上购物节活动可享受八折优惠,但需另外支付10元快递费.小明妈妈活动期间购买一双运动鞋的费用可表示为(B)
A.$(8a+10)$元
B.$(80\%a+10)$元
C.$(1-80\%)a$元
D.$[(1-80\%)a+10]$元

答案： B

3. 将含盐率为10%的盐水$m\ g$调配成含盐率为20%的盐水,需加盐$\frac{1}{8}m$$g$.(用含$m$的代数式表示)

答案： $\frac{1}{8}m$ 解析：设需加盐$x\ g$，则加盐后盐水中有盐$(10\%m+x)\ g$或$20\%(m+x)\ g$. 根据题意，得$10\%m+x=20\%(m+x)$，解得$x=\frac{1}{8}m$，即需加盐$\frac{1}{8}m\ g$.

4. 某工程队要修路$a\ m$,计划平均每天修$b\ m$,则计划完成此项工程的时间为$\frac{a}{b}$天.

答案： $\frac{a}{b}$

5. 一个两位数,个位上的数字为$m$,十位上的数字为$n$,用含$m、n$的代数式表示这个两位数为$10n+m$.

答案： $10n+m$

6. 一组按规律排列的数：$-2,\frac{4}{3},-\frac{8}{5},\frac{16}{7},-\frac{32}{9},…$,第$n$($n$为正整数)个数是______$(-1)^n\frac{2^{n}}{2n-1}$.

答案： $(-1)^n\frac{2n}{2n-1}$

7. 小明用火柴棒按如图所示的规律摆放下列图形,则摆放第n个图形共需要火柴棒(5n+1)根.
…

答案： $(5n+1)$ 解析：因为搭第1个图形需要6根火柴棒，$6=5+1$；搭第2个图形需要11根火柴棒，$11=5×2+1$；搭第3个图形需要16根火柴棒，$16=5×3+1$；……；所以搭第$n$个图形需要的火柴棒的根数是$5n+1$.

8. 如图,在长方形中挖去一个圆形,则阴影部分面积的表达式为$ab-\frac{1}{4}\pi a^2$.

答案： $ab-\frac{1}{4}\pi a^2$ 解析：$ab-\pi\left(\frac{a}{2}\right)^2=ab-\frac{1}{4}\pi a^2$.

9. 如图,大、小两个正方形的边长分别为$a、b$.
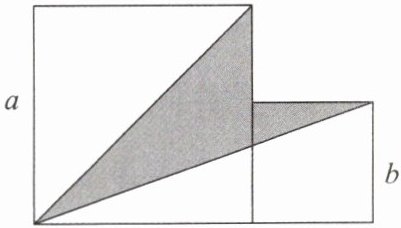
(1)用含$a、b$的代数式表示阴影部分的面积.
(2)若$|a-4|+(b-2)^{2}= 0$,求阴影部分的面积.

答案：
(1)$S_{阴影部分}=(a^2+b^2)-\left[\frac{1}{2}a^2+\frac{1}{2}b(a+b)\right]=\frac{1}{2}(a^2+b^2-ab)$.
(2)因为$|a-4|+(b-2)^2=0$，所以$a-4=0$，$b-2=0$，所以$a=4$，$b=2$，所以$S_{阴影部分}=\frac{1}{2}×(4^2+2^2-4×2)=6$.