《2025年南通小题课时作业本七年级数学上册苏科版》

25. (14分)数轴上A,B两点对应的数分别是$ -4 $,12,线段CE在数轴上运动,点C在点E的左边,且$ CE = 8 $,F是AE的中点.
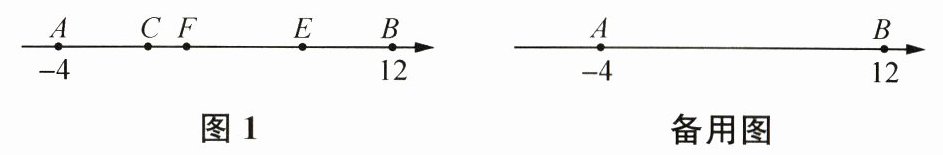
(1)如图1,当线段CE运动到点C,E均在点A,B之间时,若$ CF = 1 $,则$ AC = $______,$ BE = $______；
(2)当线段CE运动到点A在点C,E之间时.
①设AF的长为x,用含x的代数式表示$ BE = $______；
②求BE与CF的数量关系；
(3)当点C运动到数轴上表示数$ -14 $的位置时,动点P从点E出发,以每秒3个单位长度的速度向右运动,抵达点B后,立即以每秒2个单位长度的速度返回；动点P出发时,点Q从点A出发,以每秒2个单位长度的速度向终点B运动；当点Q到达点B时,P,Q两点都停止,设它们运动的时间为$ t $ s,求t为何值时,P,Q两点间的距离为1个单位长度.

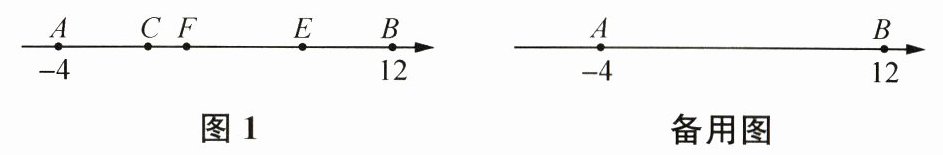
答案：
(1)6 2
(2)①16−2x
②因为CF=CE−EF=CE−AF=8−x，
所以BE=2CF.
(3)因为点C运动到数轴上表示数−14的位置，CE=8，
所以点E表示的数为−6.
当点P向数轴正方向运动，且与点Q没有相遇时，由题意，得3t+1=2t+2，解得t=1；
当点P向数轴正方向运动，且与点Q相遇后时，
由题意，得3t−1=2t+2，解得t=3；
当点P向数轴负方向运动，且与点Q没有相遇时，由题意，得2(t−6)+1+2t=16，解得t=$\frac{27}{4}$；
当点P向数轴负方向运动，且与点Q相遇后时，
由题意，得2(t−6)+2t=16+1，解得t=$\frac{29}{4}$.
综上，当t的值为1或3或$\frac{27}{4}$或$\frac{29}{4}$时，P，Q两点间的距离为1个单位长度.