《2025年南通小题课时作业本七年级数学上册苏科版》

20. (8分)(2025南京浦口月考)请把下列说理过程及理由补充完整.
已知：如图,$ \angle1 = \angle2 $,$ \angle B = \angle C $.
求证：$ \angle B + \angle BFC = 180^\circ $.
证明：因为$ \angle1 = \angle2 $(已知),
且$ \angle1 = \angle CGD $(______),
所以$ \angle2 = \angle CGD $(等量代换).
所以$ CE // BF $(______),
所以______$ = \angle C $(______).
因为$ \angle B = \angle C $(已知),
所以$ \angle BFD = \angle B $(______),
所以$ AB // CD $(______),
所以$ \angle B + \angle BFC = 180^\circ $(______).

答案： 对顶角相等
同位角相等，两直线平行
∠BFD 两直线平行，同位角相等
等量代换
内错角相等，两直线平行
两直线平行，同旁内角互补

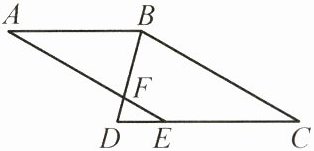
21. (8分)(2024泰州月考)如图,BD平分$ \angle ABC $,$ \angle C = 30^\circ $,$ \angle ABD = 75^\circ $,AE,BD交于点F.
(1)求证：$ AB // CD $;
(2)若$ AE // BC $,求______的度数.
请从“①$ \angle AFD $; ②$ \angle A $”中选择一项填在上面横线处(填序号),并写出求解过程.

答案：
(1)因为BD平分∠ABC，∠ABD=75°，
所以∠ABC=2∠DBC=2∠ABD=150°.
因为∠C=30°，
所以∠C+∠ABC=180°，
所以AB//CD.
(2)若选①：因为BD平分∠ABC，∠ABD=75°，所以∠DBC=∠ABD=75°.
因为AE//BC，
所以∠DFE=∠DBC=75°，
所以∠AFD=180°−75°=105°.
若选②：因为AE//BC，
所以∠ABC+∠A=180°.
又∠ABC=150°，
所以∠A=180°−150°=30°.