6. 下列说法中,错误的是( )
A.两点之间线段最短
B.对顶角相等
C.同角的补角相等
D.过一点有且只有一条直线与已知直线平行
A.两点之间线段最短
B.对顶角相等
C.同角的补角相等
D.过一点有且只有一条直线与已知直线平行
答案:
D
7. 如图,点E在AC的延长线上,下列条件中能判断$ AB // CD $的是( )
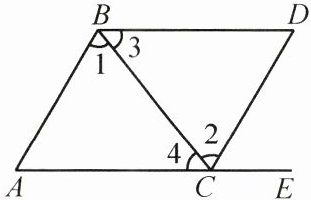
A.$ \angle3 = \angle4 $
B.$ \angle D + \angle ACD = 180^\circ $
C.$ \angle D = \angle DCE $
D.$ \angle1 = \angle2 $

A.$ \angle3 = \angle4 $
B.$ \angle D + \angle ACD = 180^\circ $
C.$ \angle D = \angle DCE $
D.$ \angle1 = \angle2 $
答案:
D
8. 如图,M是线段AB的中点,NB为MB的$ \frac{1}{4} $,$ MN = a $,则AB的长为( )
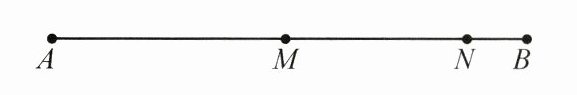
A.$ \frac{8}{3}a $
B.$ \frac{4}{3}a $
C.$ 2a $
D.$ 1.5a $
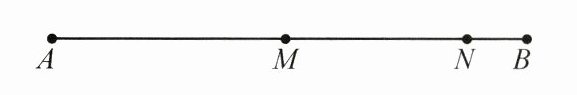
A.$ \frac{8}{3}a $
B.$ \frac{4}{3}a $
C.$ 2a $
D.$ 1.5a $
答案:
A
9. (2024南通通州月考)如图,直线AB与CD相交于点O,OE平分$ \angle BOD $,$ OE \perp OF $,若$ \angle AOC = 60^\circ $,则$ \angle BOF $的度数是( )
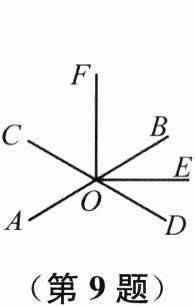
A.$ 50^\circ $
B.$ 60^\circ $
C.$ 65^\circ $
D.$ 55^\circ $

A.$ 50^\circ $
B.$ 60^\circ $
C.$ 65^\circ $
D.$ 55^\circ $
答案:
B
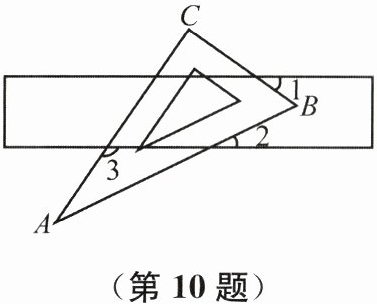
10. (2024常州期末)将一块含$ 30^\circ $角的直角三角板与一把直尺按如图所示方式摆放,$ \angle C = 90^\circ $,$ \angle A = 30^\circ $. 若$ \angle1 = \alpha^\circ $,则$ \angle3 - \angle2 $的大小为( )
A.$ 30^\circ $
B.$ 60^\circ $
C.$ (30 + \alpha)^\circ $
D.$ (30 + 2\alpha)^\circ $

A.$ 30^\circ $
B.$ 60^\circ $
C.$ (30 + \alpha)^\circ $
D.$ (30 + 2\alpha)^\circ $
答案:
D
11. (2024巴中)从五边形的一个顶点出发可以引______条对角线.
答案:
2
查看更多完整答案,请扫码查看


