8. (2024 常州溧阳期中)有理数 a,b,c 在数轴上对应的点的位置如图所示. 设 $x = a + b + c$,$y = a + b - c$,$z = a - b - c$,那么 x,y,z 计算结果中最小的是( )
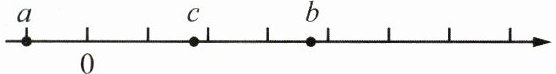
A.x
B.y
C.z
D.根据 a,b,c 的值才能确定
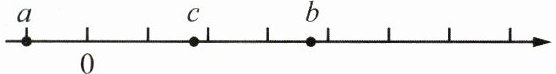
A.x
B.y
C.z
D.根据 a,b,c 的值才能确定
答案:
C
9. 若 $|a| = 5$,b 是 $-\frac{1}{3}$ 的倒数,且 $a < b$,则 $|a + b|$ 等于( )
A.8
B.2
C.8 或 2
D.$5\frac{1}{3}$
A.8
B.2
C.8 或 2
D.$5\frac{1}{3}$
答案:
A
10. 有机化学中“烷烃”的分子式如 $CH_{4}$,$C_{2}H_{6}$,$C_{3}H_{8}$……可分别按下图对应展开,则分子式 $C_{100}H_{m}$ 中 m 的值是( )

A.200
B.202
C.302
D.300

A.200
B.202
C.302
D.300
答案:
B
11. (2024 南京)如果有理数 a,b 满足______,那么 a,b 互为相反数.
答案:
$a + b = 0$
12. (2025 南京模拟)比较大小:$-\frac{3}{7}$______$-\frac{2}{3}$.(填“>”“<”或“=”)
答案:
>
13. 计算:$-1^{2} + (-1)^{3} - (-1)^{4} = $______.
答案:
$-3$
14. (2024 无锡梁溪月考)绝对值小于 4 的所有整数的和是______.
答案:
0
15. 若 m,n 满足 $|m - 2| + (n - 1)^{2} = 0$,则 $m^{n}$ 的值为______.
答案:
2
16. (2024 南京建邺期中)若数轴上点 A 表示的数是 -4,则与点 A 相距 5 个单位长度的点表示的数是______.
答案:
1或$-9$
17. 用“※”定义一种新运算:对于任意有理数 a 和 b,规定 $a※b = ab^{2} + a$,如:$1※3 = 1×3^{2} + 1 = 10$,则 $(-2)※3$ 的值为______.
答案:
$-20$
18. 已知整数 $a_{1}$,$a_{2}$,$a_{3}$,$a_{4}$……满足下列条件:$a_{1} = 0$,$a_{2} = -|a_{1} + 1|$,$a_{3} = -|a_{2} + 2|$,$a_{4} = -|a_{3} + 3|$,…,以此类推,则 $a_{2024}$ 的值为______.
答案:
$-1012$
查看更多完整答案,请扫码查看


